题目内容
桌面上放有
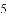
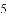
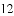
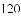
练习册系列答案
相关题目
在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共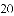
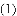
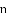
摸球的次数 |
|
|
|
|
|
|
摸到白球的次数 |
|
|
|
|
|
|
摸到白球的概率 |
|
|
|
|
|
|
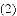

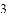
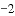
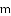
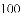
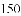
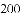
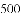
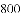
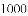
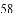
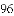
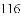
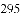
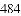
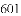
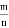
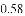
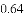
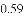
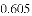
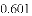
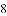
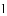
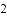
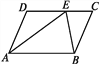
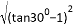 等于( )
等于( )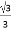 B.
B. 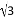 -1 C.
-1 C.