题目内容
 如图,?ABCD中,AB=6cm,BC=10cm,AE⊥BC,垂足为E,若BE:EC=1:4,求AF的长.
如图,?ABCD中,AB=6cm,BC=10cm,AE⊥BC,垂足为E,若BE:EC=1:4,求AF的长.考点:平行四边形的性质
专题:
分析:首先根据BE:EC=1:4计算出BE长,然后再根据勾股定理计算出AE长,根据平行四边形的面积公式S平行四边形ABCD=BC•AE=DC•AF可得10×4
=6•AF,再解即可.
| 2 |
解答:解:∵BC=10cm,BE:EC=1:4,
∴BE=10×
=2(cm),
∵AE⊥BC,AB=6cm,
∴AE=
=
=4
(cm),
∵四边形ABCD是平行四边形,
∴AB=CD,
∵S平行四边形ABCD=BC•AE=DC•AF,
∴10×4
=6•AF,
解得AF=
cm.
∴BE=10×
| 1 |
| 5 |
∵AE⊥BC,AB=6cm,
∴AE=
| 62-22 |
| 32 |
| 2 |
∵四边形ABCD是平行四边形,
∴AB=CD,
∵S平行四边形ABCD=BC•AE=DC•AF,
∴10×4
| 2 |
解得AF=
20
| ||
| 3 |
点评:此题主要考查了平行四边形的性质,勾股定理的应用,关键是掌握平行四边形的面积公式.

练习册系列答案
相关题目
 如图,正五边形ABCDE内接于⊙O,连接对角线AC,AD,则下列判断中错误的是( )
如图,正五边形ABCDE内接于⊙O,连接对角线AC,AD,则下列判断中错误的是( )| A、BC∥AD |
| B、∠BAE=3∠CAD |
| C、△BAC≌△EAD |
| D、AC=2CD |
 有一个数值转换器,其工作原理如图所示,若输入2,则输出的结果是( )
有一个数值转换器,其工作原理如图所示,若输入2,则输出的结果是( )| A、-8 | B、-6 | C、8 | D、10 |
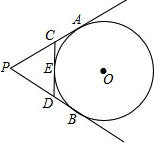 如图,PA,PB切⊙O于A,B两点,CD切⊙O于点E,交PA,PB于C,D,若⊙O的半径为r,△PCD的周长等于3r,则tan
如图,PA,PB切⊙O于A,B两点,CD切⊙O于点E,交PA,PB于C,D,若⊙O的半径为r,△PCD的周长等于3r,则tan 如图,射线OA∥CD,射线OB∥CD,∠AOC=
如图,射线OA∥CD,射线OB∥CD,∠AOC= 如图,AD∥BC.
如图,AD∥BC.