Question

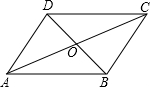如图，在?ABCD中，对角线AC、BD相交于点O．如果AB=8，AC=14，BD=x，那么x的取值范围是

 

．

Answer 1

考点：平行四边形的性质,三角形三边关系

专题：计算题

分析：根据平行四边形的性质求出OA、OC，根据三角形的三边关系定理得到AB-OA＜

1

2

x＜AB+OA，代入求出即可．

解答：解：∵ABCD是平行四边形，AB=8，AC=14，
∴OA=

1

2

AC=7，OB=

1

2

BD=

1

2

x，
∴8-7＜

1

2

x＜8+7，即2＜x＜30．
故答案为：2＜x＜30．

点评：此题考查了平行四边形的性质及三角形三边关系定理，有关“对角线范围”的题，应联系“三角形两边之和、差与第三边关系”知识点来解决．