题目内容
正数a、b、c满足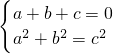
，则ab的最大值为________．
50（3-2
）
分析：根据踢中限定条件，可以a，b，c为边作一直角三角形，周长为一定值，当三角形是等腰直角三角形时面积最大．也即ab之积最大．列出方程进行求解．
解答：以a、b、c为边可作一个直角三角形ABC，其周长为10是一定值，故这样的直角三角形中等腰直角三角形的面积最大，可解得：a=b=5（2-），c=10（-1），所以最大值ab=50（3-2），故答案为50（3-2）．
点评：本题考查勾股定理的应用，以及利用勾股定理解各边长的能力．
）分析：根据踢中限定条件，可以a，b，c为边作一直角三角形，周长为一定值，当三角形是等腰直角三角形时面积最大．也即ab之积最大．列出方程进行求解．
解答：以a、b、c为边可作一个直角三角形ABC，其周长为10是一定值，故这样的直角三角形中等腰直角三角形的面积最大，可解得：a=b=5（2-
），c=10（-1），所以最大值ab=50（3-2），故答案为50（3-2）．点评：本题考查勾股定理的应用，以及利用勾股定理解各边长的能力．
练习册系列答案
相关题目
若正数a、b、c满足不等式组
，则a、b、c大小关系是（ ）
|
| A、a＜b＜c | B、b＜c＜a |
| C、c＜a＜b | D、不确定 |
+b+c的正方形来研究．