题目内容
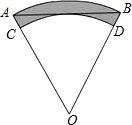 如图,扇形AOB中,∠AOB=60°,弧
如图,扇形AOB中,∠AOB=60°,弧 |
| CD |
 |
| CD |
分析:利用切线的性质和等边三角形的判定方法得到△OAB是一个等边三角形,求出其AB边上的高就是小扇形的母线长,然后利用扇形的面积计算方法算出两扇形的面积的差即为阴影部分的面积.
解答: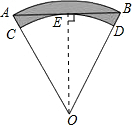 解:作OE⊥AB于E,
解:作OE⊥AB于E,
∵弦AB与
相切,
∴OE=OC=OD,
∵OA=OB,∠AOB=60°,
∴△AOB是等边三角形,
∴∠AOE=30°,AE=EB=
AB,
∴在Rt△AEO中,
0E=AE÷tan∠AOE
=2÷
=2
,
S阴影部分=S扇形OAB-S扇形OCD
=
=
π.
故答案为:
π.
 解:作OE⊥AB于E,
解:作OE⊥AB于E,∵弦AB与
 |
| CD |
∴OE=OC=OD,
∵OA=OB,∠AOB=60°,
∴△AOB是等边三角形,
60π×42-60π×(2
| ||
| 360 |
∴∠AOE=30°,AE=EB=
| 1 |
| 2 |
∴在Rt△AEO中,
0E=AE÷tan∠AOE
=2÷
| ||
| 3 |
=2
| 3 |
S阴影部分=S扇形OAB-S扇形OCD
=
60π×42-60π×(2
| ||
| 360 |
=
| 2 |
| 3 |
故答案为:
| 2 |
| 3 |
点评:本题考查了等边三角形的判定及性质、扇形的面积计算方法及切线的性质,解决本题的关键是求出小扇形的半径.

练习册系列答案
相关题目
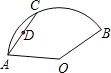 如图,扇形AOB中,∠AOB=150°,AC=AO=6,D为AC的中点,当弦AC沿扇形运动时,点D所经过的路程为( )
如图,扇形AOB中,∠AOB=150°,AC=AO=6,D为AC的中点,当弦AC沿扇形运动时,点D所经过的路程为( )| A、3π | ||||
B、
| ||||
C、
| ||||
| D、4π |
 15、如图,扇形AOB中,OA=12cm,OA⊥OB,O1是OA上一点,以O1为圆心、O1A为半径的半圆和以OB为直径的半圆O2相外切,则半圆O1的半径为
15、如图,扇形AOB中,OA=12cm,OA⊥OB,O1是OA上一点,以O1为圆心、O1A为半径的半圆和以OB为直径的半圆O2相外切,则半圆O1的半径为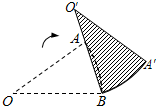 如图,扇形AOB中,OA=10,∠AOB=36°.若将此扇形绕点B顺时针旋转,得一新扇形A′O′B,其中A点在O′B上,则点O的运动路径长为
如图,扇形AOB中,OA=10,∠AOB=36°.若将此扇形绕点B顺时针旋转,得一新扇形A′O′B,其中A点在O′B上,则点O的运动路径长为

