题目内容
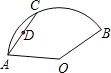如图，扇形AOB中，∠AOB=150°，AC=AO=6，D为AC的中点，当弦AC沿扇形运动时，点D所经过的路程为（ ）| A、3π | ||||
B、
| ||||
C、
| ||||
| D、4π |
分析：由垂径定理求得线段OD的长也就是点D所经过圆弧路径的半径，然后求得路径的圆心角，利用弧长的计算公式计算即可．
解答：
解：∵D为AC的中点，AC=AO=6，
∴OD⊥AC，
∴AD=
AO，
∴∠AOD=30°，OD=3
，
同理可得：∠BOE=30°，
∴∠DOE=150°-60°=90°
∴点D所经过路径长为：
=
=
π．
故选C．
解：∵D为AC的中点，AC=AO=6，∴OD⊥AC，
∴AD=
| 1 |
| 2 |
∴∠AOD=30°，OD=3
| 3 |
同理可得：∠BOE=30°，
∴∠DOE=150°-60°=90°
∴点D所经过路径长为：
| nπr |
| 180 |
90π×3
| ||
| 180 |
3
| ||
| 2 |
故选C．
点评：本题考查了垂径定理、解直角三角形、弧长的计算等知识，解决本题的关键是根据题意确定点运动的路径是什么．
练习册系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
15、如图，扇形AOB中，OA=12cm，OA⊥OB，O1是OA上一点，以O1为圆心、O1A为半径的半圆和以OB为直径的半圆O2相外切，则半圆O1的半径为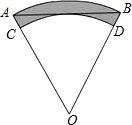
如图，扇形AOB中，∠AOB=60°，弧
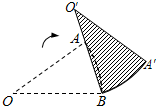如图，扇形AOB中，OA=10，∠AOB=36°．若将此扇形绕点B顺时针旋转，得一新扇形A′O′B，其中A点在O′B上，则点O的运动路径长为
