题目内容
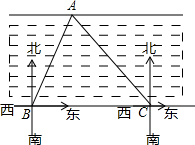（2013•延安二模）如图，某施工单位为测得某河段的宽度，测量员先在河对岸边取一点A，再在河这边沿河取两点B、C，在点B处测得点A在北偏东30°方向上，在点C处测得点A在西北方向上，量得BC长为200米，请你求出该河段的宽度（结果保留根号）．分析：作AD⊥BC于点D，易得AD=CD，进而可得BD=BC-CD=200-AD．在Rt△ABD中，通过解直角三角形求解．
解答：
解：过点A作AD⊥BC于点D．
根据题意，∠ABC=90°-30°=60°，∠ACD=45°，
∴∠CAD=45°，
∴∠ACD=∠CAD，
∴AD=CD，
∴BD=BC-CD=200-AD．
在Rt△ABD中，tan∠ABD=
，
∴AD=BD•tan∠ABD=（200-AD）•tan60°=（200-AD）•
，
∴AD+
AD=200
，
∴AD=
=300-100
．
答：该河段的宽度为（300-100
）米．
解：过点A作AD⊥BC于点D． 根据题意，∠ABC=90°-30°=60°，∠ACD=45°，
∴∠CAD=45°，
∴∠ACD=∠CAD，
∴AD=CD，
∴BD=BC-CD=200-AD．
在Rt△ABD中，tan∠ABD=
| AD |
| BD |
∴AD=BD•tan∠ABD=（200-AD）•tan60°=（200-AD）•
| 3 |
∴AD+
| 3 |
| 3 |
∴AD=
200
| ||
|
| 3 |
答：该河段的宽度为（300-100
| 3 |
点评：此题考查解直角三角形的应用，通过作辅助线构造直角三角形，把实际问题转化为数学问题是解题的关键．
练习册系列答案
相关题目
（2013•延安二模）如图，AB是⊙O的直径，C是⊙O上的一点，若AC=8cm，AB=10cm，CD⊥BC于点D，则BD的长（ ）
（2013•延安二模）如图所示的运算程序中，若开始输入的x值为80，我们发现第一次输出的结果为40，第二次输出的结果为20，…，则第2012次输出的结果为