题目内容
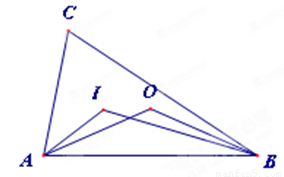
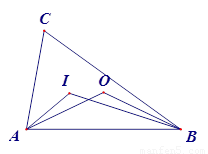
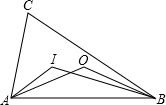 如图,点I和O分别是△ABC的内心和外心,∠AOB=100°,则∠AIB=( )
如图,点I和O分别是△ABC的内心和外心,∠AOB=100°,则∠AIB=( )分析:根据圆周角定理求出∠C,求出∠CAB+∠CBA,根据三角形内心求出∠IAB+∠IBA,根据三角形内角和定理求出即可.
解答:解:∵点O是△ABC的外心,∠AOB=100°,
∴∠C=
∠AOB=50°,
∴∠CAB+∠CBA=180°-∠C=130°,
∵点I是△ABC的内心,
∴∠IAB=
∠CAB,∠IBA=
∠CBA,
∴∠IAB+∠IBA=
×(∠CAB+∠CBA)=65°,
∴∠AIB=180°-(∠IAB+∠IBA)=180°-65°=115°,
故选C.
∴∠C=
| 1 |
| 2 |
∴∠CAB+∠CBA=180°-∠C=130°,
∵点I是△ABC的内心,
∴∠IAB=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠IAB+∠IBA=
| 1 |
| 2 |
∴∠AIB=180°-(∠IAB+∠IBA)=180°-65°=115°,
故选C.
点评:本题考查了三角形内角和定理,三角形的外接圆和三角形的内切圆的应用,关键是求出∠IAB+∠IBA的度数.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
如图,点I和O分别是△ABC的内心和外心,则∠AIB和∠AOB的关系为( )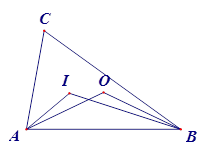
| A.∠AIB=∠AOB | B.∠AIB≠∠AOB |
| C.4∠AIB-∠AOB=360° | D.2∠AOB-∠AIB=180° |
 (2013•武汉模拟)如图,点I和O分别是△ABC的内心和外心,则∠AIB和∠AOB的关系为( )
(2013•武汉模拟)如图,点I和O分别是△ABC的内心和外心,则∠AIB和∠AOB的关系为( )