题目内容
 如图,点A、B在双曲线y=
如图,点A、B在双曲线y=| 4 |
| x |
| AB |
| BC |
| 2 |
| 1 |
| 1 |
| x |
考点:反比例函数综合题
专题:综合题
分析:过点A,点B,点D分别作OC的垂线AE,BF,DG,垂足分别为E,F,G,利用反比例函数k的几何意义求出三角形ODG与三角形OAE的面积之比,由两三角形相似,确定出相似比,即DG与AE之比,设yD=DG=a,则有yA=AE=2a,进而表示出G与OE,由三角形AEC与三角形BFC相似,且AB:BC=2:1,求出AE与BF之比,表示出B的纵坐标,得到B的横坐标,进而表示出GF与EF,三角形ADB面积=四边形AOFB面积-四边形DOBF面积=三角形AOE面积+四边形AEFB面积-三角形ODG面积-四边形DGFB面积,求出即可.
解答: 解:过点A,点B,点D分别作OC的垂线AE,BF,DG,垂足分别为E,F,G,
解:过点A,点B,点D分别作OC的垂线AE,BF,DG,垂足分别为E,F,G,
∵S△ODG=
OG•DG=
xD•yD=
,S△OAE=
OE•AE=
xA•yA=2,
∴S△ODG:S△OAE=1:4,
∵△ODG∽△OAE,
∴DG:AE=1:2,
设yD=DG=a,则有yA=AE=2a,
∴OG=xD=
=
,OE=xA=
=
,
∵△AEC∽△BFC,AB:BC=2:1,
∴AE:BF=3:1,即yB=BF=
=
a,
∴OF=xB=
=
=
,
∴GF=OF-OG=
-
=
,EF=OF-OE=
-
=
,
∴S△ABD=S四边形AOFB-S四边形DOFB
=S△OAE+S四边形AEFB-S△ODG-S四边形DGFB
=2+
(AE+BF)•EF-
-
(DG+BF)•GF
=2+
(2a+
a)•
-
-
(a+
a)•
=2+
-
-
=
.
故答案为:
.
 解:过点A,点B,点D分别作OC的垂线AE,BF,DG,垂足分别为E,F,G,
解:过点A,点B,点D分别作OC的垂线AE,BF,DG,垂足分别为E,F,G,∵S△ODG=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴S△ODG:S△OAE=1:4,
∵△ODG∽△OAE,
∴DG:AE=1:2,
设yD=DG=a,则有yA=AE=2a,
∴OG=xD=
| 1 |
| yD |
| 1 |
| a |
| 4 |
| yA |
| 2 |
| a |
∵△AEC∽△BFC,AB:BC=2:1,
∴AE:BF=3:1,即yB=BF=
| AE |
| 3 |
| 2 |
| 3 |
∴OF=xB=
| 4 |
| yB |
| 12 |
| 2a |
| 6 |
| a |
∴GF=OF-OG=
| 6 |
| a |
| 1 |
| a |
| 5 |
| a |
| 6 |
| a |
| 2 |
| a |
| 4 |
| a |
∴S△ABD=S四边形AOFB-S四边形DOFB
=S△OAE+S四边形AEFB-S△ODG-S四边形DGFB
=2+
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=2+
| 1 |
| 2 |
| 2 |
| 3 |
| 4 |
| a |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |
| 5 |
| a |
=2+
| 16 |
| 3 |
| 1 |
| 2 |
| 25 |
| 6 |
=
| 8 |
| 3 |
故答案为:
| 8 |
| 3 |
点评:此题属于反比例函数综合题,涉及的知识有:相似三角形的判定与性质,坐标与图形性质,反比例函数k的几何意义,以及四边形与三角形面积求法,熟练掌握反比例函数的性质是解本题的关键.

练习册系列答案
相关题目
 如图所示,将平面图形绕轴旋转一周,得到的几何体是( )
如图所示,将平面图形绕轴旋转一周,得到的几何体是( )A、 |
B、 |
C、 |
D、 |

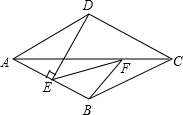 如图,在边长为6的菱形ABCD中,DE⊥AB于点E,并且点E是AB的中点,点F在线段AC上运动,则EF+FB的最小值是
如图,在边长为6的菱形ABCD中,DE⊥AB于点E,并且点E是AB的中点,点F在线段AC上运动,则EF+FB的最小值是