题目内容
 如图,∠ABC=90°,O为射线BC上一点,以点O为圆心,BO长的一半为半径作⊙O,当射线BA绕点B按顺时针方向旋转一定的角度后与⊙O相切,则旋转的角度为(小于180°)
如图,∠ABC=90°,O为射线BC上一点,以点O为圆心,BO长的一半为半径作⊙O,当射线BA绕点B按顺时针方向旋转一定的角度后与⊙O相切,则旋转的角度为(小于180°)
- A.30°
- B.60°
- C.30°或120°
- D.60°或120°
D
分析:将AB绕B点旋转到与圆相切的位置,如图:切点分别为M、N,依题意BO长为直径,OM为半径;在Rt△BOM中可求∠MBO的度数,根据圆的对称性得∠NBO=∠MBO,由此可求两个旋转角度数.
解答: 解:设AB绕B点旋转过程中,与⊙O分别相切于M、N两点,
解:设AB绕B点旋转过程中,与⊙O分别相切于M、N两点,
由切线的性质可知∠OMB=∠ONB=90°;
在Rt△BOM中,BO=2MO,
∴∠MBO=30°,
∠ABM=90°-∠MBO=60°,
∠ABN=90°+∠NBO=120°,
即:旋转角为60°或120°.
故选D.
点评:本题考查了旋转与圆的综合题,解题时需要形数结合,根据切线的性质,圆的对称性求解.
分析:将AB绕B点旋转到与圆相切的位置,如图:切点分别为M、N,依题意BO长为直径,OM为半径;在Rt△BOM中可求∠MBO的度数,根据圆的对称性得∠NBO=∠MBO,由此可求两个旋转角度数.
解答:
 解:设AB绕B点旋转过程中,与⊙O分别相切于M、N两点,
解:设AB绕B点旋转过程中,与⊙O分别相切于M、N两点,由切线的性质可知∠OMB=∠ONB=90°;
在Rt△BOM中,BO=2MO,
∴∠MBO=30°,
∠ABM=90°-∠MBO=60°,
∠ABN=90°+∠NBO=120°,
即:旋转角为60°或120°.
故选D.
点评:本题考查了旋转与圆的综合题,解题时需要形数结合,根据切线的性质,圆的对称性求解.

练习册系列答案
相关题目
 3、如图,∠ABC=90°,BD⊥AC,垂足为D,则能表示点到直线(或线段)的距离的线段有( )
3、如图,∠ABC=90°,BD⊥AC,垂足为D,则能表示点到直线(或线段)的距离的线段有( ) 如图,∠ABC=90°,BC=4,AC=5,以BC为公共边的直角△BCD与△ABC相似,且D、A在BC的两侧,求BD的长.(只要写出两种情况即可)
如图,∠ABC=90°,BC=4,AC=5,以BC为公共边的直角△BCD与△ABC相似,且D、A在BC的两侧,求BD的长.(只要写出两种情况即可)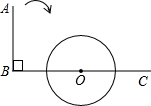 如图,∠ABC=90°,O为射线BC上一点,以点O为圆心、
如图,∠ABC=90°,O为射线BC上一点,以点O为圆心、 (2012•大兴区二模)已知:如图,∠ABC=90°,DC⊥BC,E,F为BC上两点,且BE=CF,AB=DC.
(2012•大兴区二模)已知:如图,∠ABC=90°,DC⊥BC,E,F为BC上两点,且BE=CF,AB=DC. 如图,∠ABC=90°,AB=4cm,BC=2cm,C到AB的距离为
如图,∠ABC=90°,AB=4cm,BC=2cm,C到AB的距离为