题目内容
无论k为何值时，直线y=2kx+1和抛物线y=x2+x+k
- A.都有一个公共点
- B.都有两个公共点
- C.没有公共点
- D.公共点个数不确定
B
分析：将直线y=2kx+1代入抛物线y=x2+x+k，建立关于x的一元二次方程，再利用根的判别式进行解答．
解答：将直线y=2kx+1代入抛物线y=x2+x+k，得x2+x+k=2kx+1，
整理，得x2+（1-2k）x+k-1=0，
则△=（1-2k）2-4（k-1）=4k2-8k+5=4（k2-2k）+5=4（k2-2k+1）+1=4（k-1）2+1＞0，
可见，无论k取何值，直线y=2kx+1和抛物线y=x2+x+k都有两个公共点．
故选B．
点评：本题考查了一元二次方程根的判别式，利用判别式进行计算时要将一元二次方程化为一般形式．
分析：将直线y=2kx+1代入抛物线y=x2+x+k，建立关于x的一元二次方程，再利用根的判别式进行解答．
解答：将直线y=2kx+1代入抛物线y=x2+x+k，得x2+x+k=2kx+1，
整理，得x2+（1-2k）x+k-1=0，
则△=（1-2k）2-4（k-1）=4k2-8k+5=4（k2-2k）+5=4（k2-2k+1）+1=4（k-1）2+1＞0，
可见，无论k取何值，直线y=2kx+1和抛物线y=x2+x+k都有两个公共点．
故选B．
点评：本题考查了一元二次方程根的判别式，利用判别式进行计算时要将一元二次方程化为一般形式．
练习册系列答案
相关题目
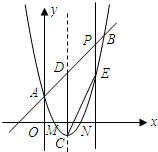作x轴的垂线交抛物线于点E，使四边形DCEP为平行四边形？若存在，请求出该平行四边形的面积；若不存在，说明理由．