题目内容
无论k为何值时，直线y=2kx+1和抛物线y=x2+x+k（ ）
| A．都有一个公共点 | B．都有两个公共点 |
| C．没有公共点 | D．公共点个数不确定 |
将直线y=2kx+1代入抛物线y=x2+x+k，得x2+x+k=2kx+1，
整理，得x2+（1-2k）x+k-1=0，
则△=（1-2k）2-4（k-1）=4k2-8k+5=4（k2-2k）+5=4（k2-2k+1）+1=4（k-1）2+1＞0，
可见，无论k取何值，直线y=2kx+1和抛物线y=x2+x+k都有两个公共点．
故选B．
整理，得x2+（1-2k）x+k-1=0，
则△=（1-2k）2-4（k-1）=4k2-8k+5=4（k2-2k）+5=4（k2-2k+1）+1=4（k-1）2+1＞0，
可见，无论k取何值，直线y=2kx+1和抛物线y=x2+x+k都有两个公共点．
故选B．
练习册系列答案
百分学生作业本题练王系列答案
相关题目
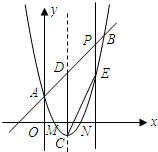作x轴的垂线交抛物线于点E，使四边形DCEP为平行四边形？若存在，请求出该平行四边形的面积；若不存在，说明理由．