题目内容
 如图,BF=CE,BE⊥AC于点E,CF⊥AB于点F,BE和CF相交于点D.求证:AD是∠BAC的平分线.
如图,BF=CE,BE⊥AC于点E,CF⊥AB于点F,BE和CF相交于点D.求证:AD是∠BAC的平分线.考点:全等三角形的判定与性质
专题:证明题
分析:根据AAS先证明△BDF≌△CDE,得出DE=DF,根据角平分线的性质定理的逆定理可得出AD是∠BAC的平分线.
解答:证明:∵BE⊥AC,CF⊥AB,
∴∠BFD=∠CED=90°,
在△BDF和△CDE中,
,
∴△BDF≌△CDE(AAS),
∴DE=DF(全等三角形的对应边相等),
∵BE⊥AC,CF⊥AB,
∴AD是∠BAC的平分线.
∴∠BFD=∠CED=90°,
在△BDF和△CDE中,
|
∴△BDF≌△CDE(AAS),
∴DE=DF(全等三角形的对应边相等),
∵BE⊥AC,CF⊥AB,
∴AD是∠BAC的平分线.
点评:本题考查了全等三角形的判定和性质,判断两个三角形全等的方法:SSS,SAS,ASA,AAS,还有直角三角形的判定定理:HL.

练习册系列答案
相关题目
 已知,如图,折叠长方形的一边AD使点D落在BC边的点F处,折痕为AE,已知AB=6cm,BC=10cm,求EC的长.
已知,如图,折叠长方形的一边AD使点D落在BC边的点F处,折痕为AE,已知AB=6cm,BC=10cm,求EC的长.
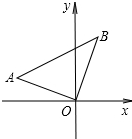 已知,∠ACB=90°,∠A=60°,点A的坐标(-
已知,∠ACB=90°,∠A=60°,点A的坐标(- 直线y=-x+b与双曲线y=-
直线y=-x+b与双曲线y=-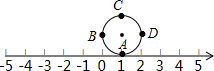 如图所示,圆的周长为4个单位长度,在圆的4等分点处标上字母A,B,C,D,先将圆周上的字母A对应的点与数轴的数字1所对应的点重合,若将圆沿着数轴向左滚动.那么数轴上的-2014所对应的点将与圆周上字
如图所示,圆的周长为4个单位长度,在圆的4等分点处标上字母A,B,C,D,先将圆周上的字母A对应的点与数轴的数字1所对应的点重合,若将圆沿着数轴向左滚动.那么数轴上的-2014所对应的点将与圆周上字