题目内容
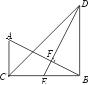
如图所示,在△ACB与△DBC中,∠ACB=∠DBC=90°,点E是BC的中点,EF⊥AB,垂足为F,且AB=DE.(1)猜想△DBC的形状?并说明理由;
(2)若BD=8cm,求AC的长.
答案:
解析:
解析:
| (1)△DBC为等腰直角三角形.
证明:∵∠FEB+∠FBE=90°,∠A+∠CBA=90°, ∴∠A=∠FEB. 又∵∠ACB=∠DBE=90°,AB=DE, ∴△ACB≌△EBD.∴BC=BD,又∠DBC=90°. ∴△DBC为等腰直角三角形. (2)∵BD=8cm,∴BC=8cm. ∴BE= 由△ACB≌△EBD,∴AC=BE,∴AC=4cm. |

练习册系列答案
相关题目
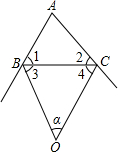 如图所示,在△ABC中,∠ABC和∠ACB的外角平分线交于点O,设∠BOC=α,则∠A等于( )
如图所示,在△ABC中,∠ABC和∠ACB的外角平分线交于点O,设∠BOC=α,则∠A等于( )| A、90°-2α | ||
B、90°-
| ||
| C、180°-2α | ||
D、180°-
|
 32、如图所示,在△ABC中,∠ACB=90°,AD=AC,BE=BC,D、E两点在AB边上,求∠DCE的度数.
32、如图所示,在△ABC中,∠ACB=90°,AD=AC,BE=BC,D、E两点在AB边上,求∠DCE的度数. (2011•利川市一模)已知大圆⊙O2经过小圆⊙O1的圆心,两圆相交于A、B两点,D点在小圆上,C点在大圆上,如图所示.如果∠ACB=48°,则∠ADB等于
(2011•利川市一模)已知大圆⊙O2经过小圆⊙O1的圆心,两圆相交于A、B两点,D点在小圆上,C点在大圆上,如图所示.如果∠ACB=48°,则∠ADB等于 如图所示,在△ABC中,∠ACB为直角,∠CAD的角平分线交BC的延长线于点E,若∠B=35°,求∠BAE和∠E的度数.
如图所示,在△ABC中,∠ACB为直角,∠CAD的角平分线交BC的延长线于点E,若∠B=35°,求∠BAE和∠E的度数.