题目内容
 (2011•利川市一模)已知大圆⊙O2经过小圆⊙O1的圆心,两圆相交于A、B两点,D点在小圆上,C点在大圆上,如图所示.如果∠ACB=48°,则∠ADB等于
(2011•利川市一模)已知大圆⊙O2经过小圆⊙O1的圆心,两圆相交于A、B两点,D点在小圆上,C点在大圆上,如图所示.如果∠ACB=48°,则∠ADB等于66°
66°
.分析:连接AO1,BO1,根据圆内接四边形的性质得到∠ACB+∠AO1B=180°,再根据圆周角定理即可得到∠ADB的度数.
解答: 解:连接AO1,BO1,
解:连接AO1,BO1,
∵四边形AO1BC内接与⊙O2,
∴∠ACB+∠AO1B=180°,
∵∠ACB=48°,
∴∠AO1B=180°-48°=132°,
∴∠ADB=
∠AO1B=
×132°=66°.
故答案为:66°.
 解:连接AO1,BO1,
解:连接AO1,BO1,∵四边形AO1BC内接与⊙O2,
∴∠ACB+∠AO1B=180°,
∵∠ACB=48°,
∴∠AO1B=180°-48°=132°,
∴∠ADB=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:66°.
点评:本题考查的是圆周角定理及圆内接四边形的性质,根据题意作出辅助线,.构造出圆内接四边形是解答此题的关键.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
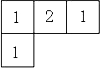 (2011•利川市一模)如图所示,是几个相同小正方体所搭成几何体的俯视图,小正方形内的数字表示在该位置的小正方体的个数.则这个几何体的主视图是( )
(2011•利川市一模)如图所示,是几个相同小正方体所搭成几何体的俯视图,小正方形内的数字表示在该位置的小正方体的个数.则这个几何体的主视图是( ) (2011•利川市一模)如图,反映的是九(3)班学生某次数学考试成绩不及格、及格、优分的人数分布直方图和扇形统计图(部分),则下列说法中不正确的是( )
(2011•利川市一模)如图,反映的是九(3)班学生某次数学考试成绩不及格、及格、优分的人数分布直方图和扇形统计图(部分),则下列说法中不正确的是( )