题目内容
12.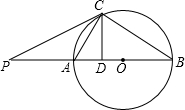 如图,AB为⊙O的直径,P为BA的延长线上一点,PC切⊙O于点C,CD⊥AB,垂足为D,且PA=4,PC=8,求tan∠ACD和sin∠P的值.
如图,AB为⊙O的直径,P为BA的延长线上一点,PC切⊙O于点C,CD⊥AB,垂足为D,且PA=4,PC=8,求tan∠ACD和sin∠P的值.
分析 如图,连接OC.∠先证明△PCA∽△PBC,得$\frac{PC}{PB}$=$\frac{PA}{PC}$,推出PB=16,AB=12,由$\frac{1}{2}$•PC•OC=$\frac{1}{2}$•PO•CD,求出CD=$\frac{24}{5}$,在Rt△COD中,利用OD=$\sqrt{O{C}^{2}-C{D}^{2}}$,求出OD,再根据tan∠ACD=$\frac{AD}{CD}$,sin∠P=$\frac{CD}{PC}$,即可解决问题.
解答 解:如图,连接OC.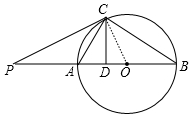
∵PA是切线,
∴OC⊥PC,
∵AB是直径,
∴∠ACB=∠PCO=90°,
∵∠B+∠BAC=90°,∠PCA+∠ACO=90°,
∵OC=OA,
∴∠OCA=∠OAC,
∴∠PCA=∠B,∵∠P=∠P,
∴△PCA∽△PBC,
∴$\frac{PC}{PB}$=$\frac{PA}{PC}$,
∴$\frac{8}{PB}$=$\frac{4}{8}$,
∴PB=16,AB=PB-PA=12,OC=OA=OB=6,PO=10,
∵CD⊥OP,
∴$\frac{1}{2}$•PC•OC=$\frac{1}{2}$•PO•CD,
∴CD=$\frac{24}{5}$,
在Rt△COD中,OD=$\sqrt{O{C}^{2}-C{D}^{2}}$=$\sqrt{{6}^{2}-(\frac{24}{5})^{2}}$=$\frac{18}{5}$,
∴AD=OA-OD=$\frac{12}{5}$,
∴tan∠ACD=$\frac{AD}{CD}$=$\frac{\frac{12}{5}}{\frac{18}{5}}$=$\frac{2}{3}$,
sin∠P=$\frac{CD}{PC}$=$\frac{\frac{24}{5}}{8}$=$\frac{3}{5}$.
点评 本题考查切线的性质、相似三角形的判定和性质、勾股定理、锐角三角函数等知识,解题的关键是灵活运用所学知识解决问题,学会添加常用辅助线,属于中考常考题型.

 已知实数a、b在数轴上对应的点如图所示,则下列式子正确的是( )
已知实数a、b在数轴上对应的点如图所示,则下列式子正确的是( )| A. | a-b>0 | B. | a+b<0 | C. | |a|<|b| | D. | a•b>0 |
| A. | 4 | B. | 6 | C. | 5 | D. | 无数 |
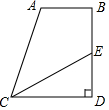 如图,AB∥CD,BD⊥CD,CE平分∠ACD,若∠CAB=100°,则∠CED的度数为50度.
如图,AB∥CD,BD⊥CD,CE平分∠ACD,若∠CAB=100°,则∠CED的度数为50度. 如图所示,将一个含30°角的直角三角板ABC绕点A旋转,使得点B,A,C′在同一条直线上,则三角板ABC旋转的角度是150°.
如图所示,将一个含30°角的直角三角板ABC绕点A旋转,使得点B,A,C′在同一条直线上,则三角板ABC旋转的角度是150°. 已知∠ADE=∠C,AG平分∠BAC交DE于F,交BC于G.
已知∠ADE=∠C,AG平分∠BAC交DE于F,交BC于G. (1)在如图所给的平面直角坐标系中,描出点A(3,4),B(0,2),C(3,-2),再顺次连接A、B、C三点;
(1)在如图所给的平面直角坐标系中,描出点A(3,4),B(0,2),C(3,-2),再顺次连接A、B、C三点;