题目内容
3.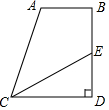 如图,AB∥CD,BD⊥CD,CE平分∠ACD,若∠CAB=100°,则∠CED的度数为50度.
如图,AB∥CD,BD⊥CD,CE平分∠ACD,若∠CAB=100°,则∠CED的度数为50度.
分析 根据两直线平行,同旁内角互补求出∠ACD,再根据角平分线的定义求出∠DCE,然后根据直角三角形两锐角互余列式计算即可得解.
解答 解:∵AB∥CD,
∴∠ACD=180°-∠CAB=180°-100°=80°,
∵CE平分∠FCD,
∴∠DCE=$\frac{1}{2}$∠ACD=$\frac{1}{2}$×80°=40°,
∵BD⊥CD,
∴∠D=90°,
∴∠CED=90°-∠DCE=90°-40°=50°.
故答案为:50.
点评 本题考查了平行线的性质,角平分线的定义,直角三角形两锐角互余的性质,熟记各性质是解题的关键.

练习册系列答案
相关题目
11.下列计算正确的是( )
| A. | (a+4)(a-4)=a2-4 | B. | (a+2)(a-1)=a2+a-2 | C. | (a+2)2=a2+4 | D. | (a+1)(a-3)=a2-3 |
 如图,AB是圆O直径,PB、PC分别与圆O相切于B、C,连接PO交圆O于D、E,CE与AD相交于F.
如图,AB是圆O直径,PB、PC分别与圆O相切于B、C,连接PO交圆O于D、E,CE与AD相交于F.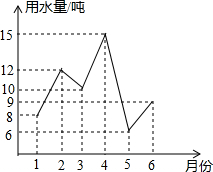 为了了解家里的用水情况,以便能更好的节约用水,小方把自己家1至6月份的用水量绘制成如图的折线图,那么小方家这6个月的月用水量最大是( )
为了了解家里的用水情况,以便能更好的节约用水,小方把自己家1至6月份的用水量绘制成如图的折线图,那么小方家这6个月的月用水量最大是( )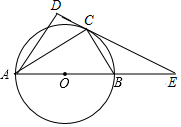 如图,点C在以AB为直径的⊙O上,过C作⊙O的切线交AB的延长线于E,
如图,点C在以AB为直径的⊙O上,过C作⊙O的切线交AB的延长线于E,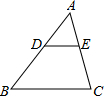 如图,在△ABC中,点D,E分别在边A B,AC上,DE∥BC,已知EC=6,$\frac{AD}{DB}=\frac{2}{3}$,则AC的长是10.
如图,在△ABC中,点D,E分别在边A B,AC上,DE∥BC,已知EC=6,$\frac{AD}{DB}=\frac{2}{3}$,则AC的长是10.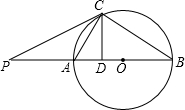 如图,AB为⊙O的直径,P为BA的延长线上一点,PC切⊙O于点C,CD⊥AB,垂足为D,且PA=4,PC=8,求tan∠ACD和sin∠P的值.
如图,AB为⊙O的直径,P为BA的延长线上一点,PC切⊙O于点C,CD⊥AB,垂足为D,且PA=4,PC=8,求tan∠ACD和sin∠P的值.