Question

（1）∵AB∥CD（已知）
∴∠

 

=

 

，∠

 

=∠

 

 （

 

　）
（2）∵AD∥BC（已知）
∴∠

 

=

 

，∠

 

=∠

 

 （

 

　）
（3）∵AD∥BC（已知）
∴∠BAD+∠

 

=180°  （

 

　）
∵AB∥CD（已知）
∴∠BCD+∠

 

=180°  （

 

　）
∴∠

 

=∠

 

（同角的补角相等）

Answer 1

考点：平行线的性质

专题：推理填空题

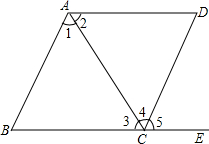
分析：（1）根据两直线平行，内错角相等，同位角相等可得∠1=∠4，∠B=∠5；
（2）根据两直线平行，内错角相等，同位角相等可得∠2=∠3，∠D=∠5；
（3）根据两直线平行，同旁内角互补可得∠BAD+∠B=180°，∠BCD+∠B=180°，再根据同角的补角相等可得∠BAD=∠BCD．

解答：解：（1）∵AB∥CD（已知），
∴∠1=∠4，∠B=∠5（两直线平行，内错角相等，同位角相等）；

（2）∵AD∥BC（已知），
∴∠2=∠3，∠D=∠5，（两直线平行，内错角相等，同位角相等）；

（3）∵AD∥BC（已知），
∴∠BAD+∠B=180° （ 两直线平行，同旁内角互补），
∵AB∥CD（已知），
∴∠BCD+∠B=180° （两直线平行，同旁内角互补）
∴∠BAD=∠BCD（同角的补角相等）．

点评：此题主要考查了平行线的性质，关键是掌握两直线平行，同旁内角互补，内错角相等，同位角相等．