题目内容
 在△ABC中,AD、BE分别为BC、AC边上的高,F为AB边上的中点,当∠C=2∠EFD时,求∠C的度数.
在△ABC中,AD、BE分别为BC、AC边上的高,F为AB边上的中点,当∠C=2∠EFD时,求∠C的度数.考点:直角三角形斜边上的中线
专题:
分析:先在RT△ABE中,由直角三角形斜边上的中线等于斜边的一半得出AF=EF=BF,根据等边对等角得到∠FAE=∠AEF,∠FEB=∠FBE.同理,在直角三角形ABD中,得出AF=DF=BF,那么∠FAD=∠ADF,∠FDB=∠FBD,再根据四边形CDFE内角和为360°得出∠C+∠CEB+∠BEF+∠ADF+∠ADC+∠EFD=360°,将∠C=2∠EFD代入得到∠C+
∠C+∠EBF+∠DAF=180°.设AD,BE交于点G.由三角形外角的性质得出∠EBF+∠DAF=∠AGE,进而得到∠C+
∠C+∠C=180°,从而求得∠C=72°.
| 1 |
| 2 |
| 1 |
| 2 |
解答: 解:在RT△ABE中,
解:在RT△ABE中,
∵F为AB中点,
∴AF=EF=BF,
∴∠FAE=∠AEF,∠FEB=∠FBE.
同理,在直角三角形ABD中,
AF=DF=BF,
∠FAD=∠ADF,∠FDB=∠FBD,
∵∠C+∠CEB+∠BEF+∠ADF+∠ADC+∠EFD=360°,
∴∠C+∠BEF+∠EFD+∠ADF+180°=360°,
∴∠C+
∠C+∠BEF+∠ADF=180°,
∴∠C+
∠C+∠EBF+∠DAF=180°.
设AD,BE交于点G.
∴∠EBF+∠DAF=∠AGE,
∵∠AEB=∠ADC,
∴∠C=∠EGA,
∴∠C+
∠C+∠C=180°,
∴∠C=72°.
 解:在RT△ABE中,
解:在RT△ABE中,∵F为AB中点,
∴AF=EF=BF,
∴∠FAE=∠AEF,∠FEB=∠FBE.
同理,在直角三角形ABD中,
AF=DF=BF,
∠FAD=∠ADF,∠FDB=∠FBD,
∵∠C+∠CEB+∠BEF+∠ADF+∠ADC+∠EFD=360°,
∴∠C+∠BEF+∠EFD+∠ADF+180°=360°,
∴∠C+
| 1 |
| 2 |
∴∠C+
| 1 |
| 2 |
设AD,BE交于点G.
∴∠EBF+∠DAF=∠AGE,
∵∠AEB=∠ADC,
∴∠C=∠EGA,
∴∠C+
| 1 |
| 2 |
∴∠C=72°.
点评:本题考查了直角三角形斜边上的中线的性质,等腰三角形的性质,多边形内角和定理,三角形外角的性质,有一定难度.

练习册系列答案
相关题目
 如图所示,它是小孔成像的原理,根据图中尺寸(AB∥CD),如果已知物体AB=30,则CD的长应是( )
如图所示,它是小孔成像的原理,根据图中尺寸(AB∥CD),如果已知物体AB=30,则CD的长应是( )| A、15 | B、30 | C、20 | D、10 |
小明和小亮口袋里面都放有五张不同的北京奥运会福娃纪念卡,则两人分别在自己口袋里摸出一张福娃都是欢欢的概率是( )


A、
| ||
B、
| ||
C、
| ||
| D、1 |
 一次函数y=-2x+4的图象如图所示,当0≤y<4时,x的取值范围是
一次函数y=-2x+4的图象如图所示,当0≤y<4时,x的取值范围是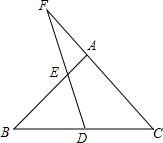 如图,已知在△ABC中,AB=AC=10,BC=16,D是BC中点,E是射线BA上一动点,直线DE交射线CA于F,当DF=DC时,求AF的值.
如图,已知在△ABC中,AB=AC=10,BC=16,D是BC中点,E是射线BA上一动点,直线DE交射线CA于F,当DF=DC时,求AF的值.