题目内容
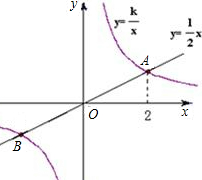
已知正比例函数y=x与反比例函数y=
的图象有一个交点的纵坐标是2．
（1）求反比例函数的解析式；
（2）当-5＜x＜-1时，反比例函数y的取值范围．
解：（1）把y=2代入y=x，得x=2，
∴正比例函数与反比例函数的交点坐标为（2，2），
把（2，2）代入反比例函数y=得k=4，
∴反比例函数的解析式为y=
；
（2）∵当x=-5时，y=-
；
当x=-1时，y=-4；
根据k=4＞0，y随x的增大而减小，
∴当-5＜x＜-1时，反比例函数y的取值范围时-4＜y＜-．
分析：（1）根据题意可得出正比例函数y=x与反比例函数y=的图象的交点坐标，再代入即可得出反比例函数的解析式；
（2）先求出当x=-5和-1时的函数值，再由反比例函数的性质得出y的取值范围．
点评：本题考查了反比例函数和一次函数的交点问题，以及用待定系数法求反比例函数的解析式，是基础知识比较简单．
∴正比例函数与反比例函数的交点坐标为（2，2），
把（2，2）代入反比例函数y=
得k=4，∴反比例函数的解析式为y=
；（2）∵当x=-5时，y=-
；当x=-1时，y=-4；
根据k=4＞0，y随x的增大而减小，
∴当-5＜x＜-1时，反比例函数y的取值范围时-4＜y＜-
．分析：（1）根据题意可得出正比例函数y=x与反比例函数y=
的图象的交点坐标，再代入即可得出反比例函数的解析式；（2）先求出当x=-5和-1时的函数值，再由反比例函数的性质得出y的取值范围．
点评：本题考查了反比例函数和一次函数的交点问题，以及用待定系数法求反比例函数的解析式，是基础知识比较简单．
练习册系列答案
相关题目
已知正比例函数y=k1x（k1≠0）与反比例函数y=
（k2≠0）的图象有一个交点的坐标为（-2，-1），则它的另一个交点的坐标是（ ）
| k2 |
| x |
| A、（2，1） |
| B、（-2，-1） |
| C、（-2，1） |
| D、（2，-1） |
横坐标为2．
如图，已知正比例函数和反比例函数的图象都经过点A（3，3）．