题目内容
【题目】知识再现:已知,如图,四边形ABCD是正方形,点M、N分别在边BC、CD上,连接AM、AN、MN,∠MAN=45°,延长CB至G使BG=DN,连接AG,根据三角形全等的知识,我们可以证明MN=BM+DN.
知识探究:(1)在如图中,作AH⊥MN,垂足为点H,猜想AH与AB有什么数量关系?并证明;
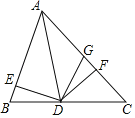
知识应用:(2)如图,已知∠BAC=45°,AD⊥BC于点D,且BD=2,AD=6,则CD的长为 ;
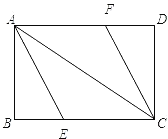
知识拓展:(3)如图,四边形ABCD是正方形,E是边BC的中点,F为边CD上一点,∠FEC=2∠BAE,AB=24,求DF的长.

【答案】(1)AB=AH, 证明见解析;(2)3;(3)8 .
【解析】
(1)先证△ABG≌△ADN,再证△GAM≌△NAM,根据GM和NM是对应边,得到AB=AH(全等三角形对应边上的高相等);
(2)作△ABD关于直线AB的对称△ABE,作△ACD关于直线AC的对称△ACF,延长EB、FC交于点G,则四边形AEGF是矩形,又AE=AD=AF,所以四边形AEGF是正方形,设设CD=x,则BG=62=4;CG=6 x;BC=2+ x,在Rt△BGC中,![]() 得x=3,所以CD的长为3.
得x=3,所以CD的长为3.
(3)过点A作![]() 交EF于点M,证明△ABE≌△AME,得到
交EF于点M,证明△ABE≌△AME,得到![]()
![]() 再证明
再证明![]() ≌
≌![]() ,设DF=x,得到EF=12+ x;FC=24 x;EC=12,在Rt△EFC中,
,设DF=x,得到EF=12+ x;FC=24 x;EC=12,在Rt△EFC中,![]() 解方程即可.
解方程即可.
(1)答:AB=AH,
证明:如图1
∵四边形ABCD是正方形,
∴![]()
∴![]()
又∵AB=AD,
∵在△ABG和△ADN中,

∴△ABG≌△ADN(SAS),
∴![]()
∵![]()
∴![]()
∴![]()
即![]()
∵在△GAM和△NAM中,
∴△GAM≌△NAM(SAS),
又∵GM和NM是对应边,
∴AB=AH(全等三角形对应边上的高相等);
(2)作△ABD关于直线AB的对称△ABE,作△ACD关于直线AC的对称△ACF,
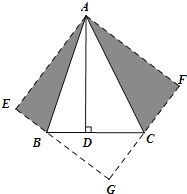
∵AD是△ABC的高,
∴![]()
∴![]()
又∵![]()
∴![]()
延长EB、FC交于点G,则四边形AEGF是矩形,
又∵AE=AD=AF
∴四边形AEGF是正方形,
由(1)、(2)知:EB=DB=2,AE=AF=AD=EG=6,
设CD=x,
∴BG=62=4;CG=6 x;BC=2+ x,
在Rt△BGC中,![]()
解得![]()
故CD的长为3.

(3)如图3,过点A作![]() 交EF于点M,
交EF于点M,
![]()
![]()
![]()
在△ABE和△AME中,

∴△ABE≌△AME(AAS),
![]()
![]()
在![]() 和
和![]() 中,
中,
![]()
![]() ≌
≌![]() ,
,
![]()
设DF=x,
∴EF=12+ x/span>;FC=24 x;EC=12,
在Rt△EFC中,![]()
解得![]()
故DF的长为8.
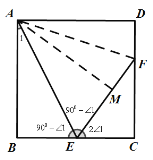
图3