题目内容
 如图所示,已知O为AC,BD,EF三线段的中点,图中有________对三角形全等.
如图所示,已知O为AC,BD,EF三线段的中点,图中有________对三角形全等.
6
分析:已知O为AC,BD,EF三线段的中点,所以四边形ABCD是平行四边形.根据平行四边形的性质及已知条件得到图中全等的三角形:△ABC≌△CDA,△ADB≌△CBD,△OAB≌△OCD,△OEA≌△OFC,△OEB≌△OFD,△OAD≌△OCB共6对.再分别进行证明.
解答:∵O为AC,BD,EF三线段的中点
∴OA=OC,OB=OD
∴四边形ABCD是平行四边形;
①△ABC≌△CDA
∵ABCD为平行四边形
∴AD=BC,∠ADC=∠ABC,AB=DC
∴△ABC≌△CDA;
②△ADB≌△CBD
∵ABCD为平行四边形
∴AD=BC,∠DAB=∠DCB,AB=DC
∴△ADB≌△CBD;
③△OAB≌△OCD
∵对角线AC与BD的交于O
∴OA=OC,OD=OB,∠AOB=∠DOC
∴△OAB≌△OCD;
④△OEA≌△OFC
∵对角线AC与BD的交于O
∴OA=OC,∠AOE=∠COF,∠AOE=∠COF
∴△OEA≌△OFC;
⑤△OEB≌△OFD
∵对角线AC与BD的交于O
∴OD=OB,∠EOB=∠FOD,OE=OF
∴△OEB≌△OFD;
⑥△OAD≌△OCB
∵对角线AC与BD的交于O
∴OA=OC,∠AOD=∠BOC,OB=OD
∴△OAD≌△OCB.
故答案为6.
点评:题考查平行四边形的性质及全等三角形的判定条件.判定两个三角形全等的一般方法有:SSS、SAS、SSA、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
分析:已知O为AC,BD,EF三线段的中点,所以四边形ABCD是平行四边形.根据平行四边形的性质及已知条件得到图中全等的三角形:△ABC≌△CDA,△ADB≌△CBD,△OAB≌△OCD,△OEA≌△OFC,△OEB≌△OFD,△OAD≌△OCB共6对.再分别进行证明.
解答:∵O为AC,BD,EF三线段的中点
∴OA=OC,OB=OD
∴四边形ABCD是平行四边形;
①△ABC≌△CDA
∵ABCD为平行四边形
∴AD=BC,∠ADC=∠ABC,AB=DC
∴△ABC≌△CDA;
②△ADB≌△CBD
∵ABCD为平行四边形
∴AD=BC,∠DAB=∠DCB,AB=DC
∴△ADB≌△CBD;
③△OAB≌△OCD
∵对角线AC与BD的交于O
∴OA=OC,OD=OB,∠AOB=∠DOC
∴△OAB≌△OCD;
④△OEA≌△OFC
∵对角线AC与BD的交于O
∴OA=OC,∠AOE=∠COF,∠AOE=∠COF
∴△OEA≌△OFC;
⑤△OEB≌△OFD
∵对角线AC与BD的交于O
∴OD=OB,∠EOB=∠FOD,OE=OF
∴△OEB≌△OFD;
⑥△OAD≌△OCB
∵对角线AC与BD的交于O
∴OA=OC,∠AOD=∠BOC,OB=OD
∴△OAD≌△OCB.
故答案为6.
点评:题考查平行四边形的性质及全等三角形的判定条件.判定两个三角形全等的一般方法有:SSS、SAS、SSA、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
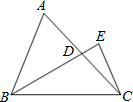 如图所示,已知D为边AC的中点,CE垂直于BD的延长线于点E,CE=2cm,S△ABC=8cm2,则线段BD的长为
如图所示,已知D为边AC的中点,CE垂直于BD的延长线于点E,CE=2cm,S△ABC=8cm2,则线段BD的长为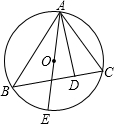 如图所示,已知AE为⊙O的直径,AD为△ABC的BC边上的高.
如图所示,已知AE为⊙O的直径,AD为△ABC的BC边上的高. 如图所示,已知AB为⊙O的直径,点P为OA上一点,弦MN过点P,且AP=2,OP=3,MP=2
如图所示,已知AB为⊙O的直径,点P为OA上一点,弦MN过点P,且AP=2,OP=3,MP=2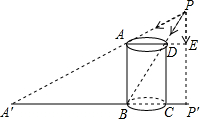 一圆柱形器皿在点光源P下的投影如图所示,已知AD为该器皿底面圆的直径,且AD=3,CD为该器皿的高,CD=4,CP′=1,点D在点P下的投影刚好位于器皿底与器皿壁的交界处,即点B处,点A在点P下的投影为A′,求点A′到CD的距离.
一圆柱形器皿在点光源P下的投影如图所示,已知AD为该器皿底面圆的直径,且AD=3,CD为该器皿的高,CD=4,CP′=1,点D在点P下的投影刚好位于器皿底与器皿壁的交界处,即点B处,点A在点P下的投影为A′,求点A′到CD的距离.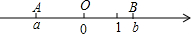 在数轴上表示a,0,1,b四个数的点如图所示,已知O为AB的中点,求a+b+
在数轴上表示a,0,1,b四个数的点如图所示,已知O为AB的中点,求a+b+