题目内容
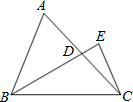 如图所示,已知D为边AC的中点,CE垂直于BD的延长线于点E,CE=2cm,S△ABC=8cm2,则线段BD的长为
如图所示,已知D为边AC的中点,CE垂直于BD的延长线于点E,CE=2cm,S△ABC=8cm2,则线段BD的长为分析:作AF⊥BD,通过三角形全等,可得AF=CE,以BD为底,AF、CE为高,表示出三角形ABC的面积,即可得出.
解答: 解:作AF⊥BD,
解:作AF⊥BD,
∵CE⊥BD,
∴∠AFD=∠CED=90°,
∵D为边AC的中点,
∴AD=CD,又∠ADF=∠CDE,
∴△AFD≌△CED(AAS),
∴AF=CE=2cm,
∵S△ABC=S△ABD+S△CBD,
=
BD×AF+
BD×CE,
∴
BD×4=8cm2,
解得,BD=4cm.
故答案为:4cm.
 解:作AF⊥BD,
解:作AF⊥BD,∵CE⊥BD,
∴∠AFD=∠CED=90°,
∵D为边AC的中点,
∴AD=CD,又∠ADF=∠CDE,
∴△AFD≌△CED(AAS),
∴AF=CE=2cm,
∵S△ABC=S△ABD+S△CBD,
=
| 1 |
| 2 |
| 1 |
| 2 |
∴
| 1 |
| 2 |
解得,BD=4cm.
故答案为:4cm.
点评:本题主要考查了三角形面积的求法,本题也可应用三角形的中线把三角形分成面积相等两部分来解答.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
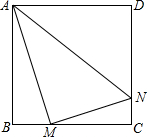 如图所示,已知正方形ABCD边长为4,点M、N分别在边BC、CD上(点M、N都不与点B、C、D重合),且AM⊥MN.
如图所示,已知正方形ABCD边长为4,点M、N分别在边BC、CD上(点M、N都不与点B、C、D重合),且AM⊥MN. 如图所示,已知D为边BC上一点,过点D画DE∥AB交AC于点E,再过点C画CF∥AD交BA的延长线于点F.
如图所示,已知D为边BC上一点,过点D画DE∥AB交AC于点E,再过点C画CF∥AD交BA的延长线于点F.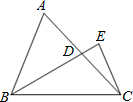 如图所示,已知D为边AC的中点,CE垂直于BD的延长线于点E,CE=2cm,S△ABC=8cm2,则线段BD的长为________.
如图所示,已知D为边AC的中点,CE垂直于BD的延长线于点E,CE=2cm,S△ABC=8cm2,则线段BD的长为________. 如图所示,已知D为边BC上一点,过点D画DE∥AB交AC于点E,再过点C画CF∥AD交BA的延长线于点F.
如图所示,已知D为边BC上一点,过点D画DE∥AB交AC于点E,再过点C画CF∥AD交BA的延长线于点F.