题目内容
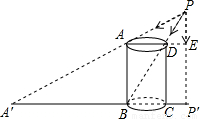
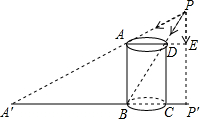一圆柱形器皿在点光源P下的投影如图所示，已知AD为该器皿底面圆的直径，且AD=3，CD为该器皿的高，CD=4，CP′=1，点D在点P下的投影刚好位于器皿底与器皿壁的交界处，即点B处，点A在点P下的投影为A′，求点A′到CD的距离．分析：根据题意知△APD∽△A′PB，△APE∽△PA′P′，然后利用相似三角形的性质求解即可．
解答：解：根据题意很明显：△APD∽△A′PB，△APE∽△PA′P′，
∴
=
=
，
又DE=CP′=1，AD=BC=3，
将各线段长度代入得：
=
，
解得：A′B=12，
∴点A′到CD的距离为A′B+BC=12+3=15．
∴
| AD |
| A′B |
| PD |
| PB |
| DE |
| BP′ |
又DE=CP′=1，AD=BC=3，
将各线段长度代入得：
| 3 |
| A′B |
| 1 |
| 4 |
解得：A′B=12，
∴点A′到CD的距离为A′B+BC=12+3=15．
点评：本题考查中心投影和相似三角形的判定与性质，解题关键是根据△APD∽△A′PB和△APE∽△PA′P′找出已知线段和被求线段的关系，难度一般．
练习册系列答案
阅读快车系列答案
相关题目
一圆柱形器皿在点光源P下的投影如图所示，已知AD为该器皿底面圆的直径，且AD=3，CD为该器皿的高，CD=4，CP′=1，点D在点P下的投影刚好位于器皿底与器皿壁的交界处，即点B处，点A在点P下的投影为A′，求点A′到CD的距离．