题目内容
我们把对称中心重合,四边分别平行的两个正方形之间的部分叫“方形环”,易知方形环四周的宽度相等.
一条直线l与方形环的边线有四个交点M、M′、N′、N.小明在探究线段MM′与N′N 的数量关系时,从点M′、N′向对边作垂线段M′E、N′F,利用三角形全等、相似及锐角三角函数等相关知识解决了问题.请你参考小明的思路解答下列问题:
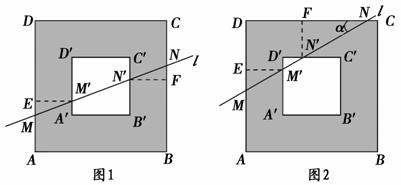
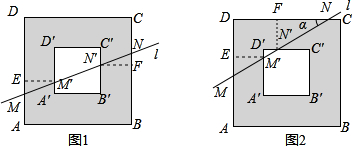
(1)当直线l与方形环的![]() 对边相交时,如图1,直线l分别交AD、A′D′、B′C′、BC于M、M′、N′、N,小明发现MM′与N′N相等,请你帮他说明理由;
对边相交时,如图1,直线l分别交AD、A′D′、B′C′、BC于M、M′、N′、N,小明发现MM′与N′N相等,请你帮他说明理由;
(2)当直线l与方形环的邻边相交时,如图2,l分别交AD、A′D′、D′C′、DC于M、M′、N′、N,l与DC的夹角为α,你认为MM′与N′N还相等吗?若相等,说明理由;若不相等,求出![]() 的值(用含α的三角函数表示).
的值(用含α的三角函数表示).
解 (1)在方形环中,∵M′E⊥AD,N′F⊥BC,AD∥BC,
∴M′E=N′F,∠M′EM=∠N′FN=90°,
∠![]() EMM′=∠FNN′,∴△MM′E≌△NN′F.
EMM′=∠FNN′,∴△MM′E≌△NN′F.
∴MM′=N′N.
(2)法一 ∵∠NFN′=∠MEM′=90°,
∠FNN′=∠EM′M=α,
∴△NFN′∽△M′EM,∴![]() =
=![]() .
.
∵M′E=N′F,∴![]() =
=![]() =tan α
=tan α![]() .
.
①当α=45°时,tan α=1,则MM′=NN′;
②![]() 当α≠45°时,MM′≠NN′,则
当α≠45°时,MM′≠NN′,则![]() =tan α
=tan α![]() .
.
法二 在方形环中,∠D=90°.
又∵M′E⊥AD,N′F⊥CD,∴M′E∥DC,N′F=M′E.
∴∠MM′E=∠N′NF=α.
在Rt△NN′F与Rt△MM′E中,
sin α=![]() ,cos α=
,cos α=![]() ,即
,即![]() =tan α
=tan α![]() .
.
① 当α=45°时,MM′=NN′;
②当α≠45°时,MM′≠NN′,则![]() =tan α
=tan α![]() .
.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
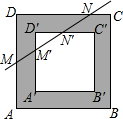 我们把对称中心重合,四边分别平行的两个正方形之间的部分叫“方形环”,已知方形环四周的宽度相等,如图,若直线l分别交方形环的邻边AD、A'D'、D'C'、DC于点M、M'、N'、N,且M为AD的中点,DN=3CN,则线段MM'与NN'的长度之比为
我们把对称中心重合,四边分别平行的两个正方形之间的部分叫“方形环”,已知方形环四周的宽度相等,如图,若直线l分别交方形环的邻边AD、A'D'、D'C'、DC于点M、M'、N'、N,且M为AD的中点,DN=3CN,则线段MM'与NN'的长度之比为
 、
、 、
、 、
、 .小明在探究线段
.小明在探究线段 与
与 的数量关系时,从点
的数量关系时,从点 、
、 ,利用三角形全等、相似及锐角三角函数等相关知识解决了问题.请你参考小明的思路解答下列问题:
,利用三角形全等、相似及锐角三角函数等相关知识解决了问题.请你参考小明的思路解答下列问题: 、
、 、
、 、
、 于
于 、
、 于
于 ,你认为
,你认为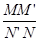 的值(用含
的值(用含
 、
、 、
、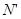 、
、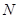 .小明在探究线段
.小明在探究线段 与
与 的数量关系时,从点
的数量关系时,从点 、
、 ,利用三角形全等、相似及锐角三角函数等相关知识解决了问题.请你参考小明的思路解答下列问题:
,利用三角形全等、相似及锐角三角函数等相关知识解决了问题.请你参考小明的思路解答下列问题: 、
、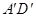 、
、 、
、 于
于 、
、 于
于 ,你认为
,你认为 的值(用含
的值(用含
 、
、 、
、 、
、 .小明在探究线段
.小明在探究线段 与
与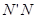 的数量关系时,从点
的数量关系时,从点 、
、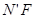 ,利用三角形全等、相似及锐角三角函数等相关知识解决了问题.请你参考小明的思路解答下列问题:
,利用三角形全等、相似及锐角三角函数等相关知识解决了问题.请你参考小明的思路解答下列问题: 、
、 、
、 、
、 于
于 、
、 于
于 ,你认为
,你认为 的值(用含
的值(用含