题目内容
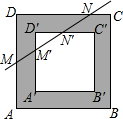 我们把对称中心重合,四边分别平行的两个正方形之间的部分叫“方形环”,已知方形环四周的宽度相等,如图,若直线l分别交方形环的邻边AD、A'D'、D'C'、DC于点M、M'、N'、N,且M为AD的中点,DN=3CN,则线段MM'与NN'的长度之比为
我们把对称中心重合,四边分别平行的两个正方形之间的部分叫“方形环”,已知方形环四周的宽度相等,如图,若直线l分别交方形环的邻边AD、A'D'、D'C'、DC于点M、M'、N'、N,且M为AD的中点,DN=3CN,则线段MM'与NN'的长度之比为分析:由题意,作M′E⊥MD,N′F⊥DN,则M′E=N′F,可得△MEM′∽△MDN,△NFN′∽△NDM,所以,
=
,
=
,整理得,
=
,又M为AD的中点,DN=3CN,代入整理可得,
=
;
| MM′ |
| MN |
| M′E |
| DN |
| NN′ |
| MN |
| N′F |
| DM |
| MM′ |
| NN′ |
| DM |
| DN |
| MM′ |
| NN′ |
| 2 |
| 3 |
解答: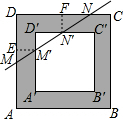 解:如图,作M′E⊥MD,N′F⊥DN,
解:如图,作M′E⊥MD,N′F⊥DN,
∵方形环四周的宽度相等,
∴M′E=N′F,
∴△MEM′∽△MDN,△NFN′∽△NDM,
∴
=
①,
=
②,
∴①÷②得:
=
,
又∵M为AD的中点,DN=3CN,
∴
=
,AD=CD,
∴
=
;
故答案为:
.
 解:如图,作M′E⊥MD,N′F⊥DN,
解:如图,作M′E⊥MD,N′F⊥DN,∵方形环四周的宽度相等,
∴M′E=N′F,
∴△MEM′∽△MDN,△NFN′∽△NDM,
∴
| MM′ |
| MN |
| M′E |
| DN |
| NN′ |
| MN |
| N′F |
| DM |
∴①÷②得:
| MM′ |
| NN′ |
| DM |
| DN |
又∵M为AD的中点,DN=3CN,
∴
| MM′ |
| NN′ |
| ||
|
∴
| MM′ |
| NN′ |
| 2 |
| 3 |
故答案为:
| 2 |
| 3 |
点评:本题主要考查了直角三角形和相似三角形的判定与性质,通过作平行线或垂线构造相似三角形,是解答本题的关键.

练习册系列答案
相关题目
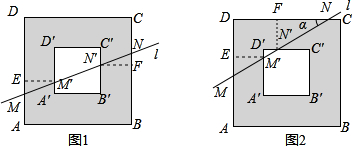

 、
、 、
、 、
、 .小明在探究线段
.小明在探究线段 与
与 的数量关系时,从点
的数量关系时,从点 、
、 ,利用三角形全等、相似及锐角三角函数等相关知识解决了问题.请你参考小明的思路解答下列问题:
,利用三角形全等、相似及锐角三角函数等相关知识解决了问题.请你参考小明的思路解答下列问题: 、
、 、
、 、
、 于
于 、
、 于
于 ,你认为
,你认为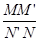 的值(用含
的值(用含
 、
、 、
、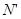 、
、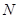 .小明在探究线段
.小明在探究线段 与
与 的数量关系时,从点
的数量关系时,从点 、
、 ,利用三角形全等、相似及锐角三角函数等相关知识解决了问题.请你参考小明的思路解答下列问题:
,利用三角形全等、相似及锐角三角函数等相关知识解决了问题.请你参考小明的思路解答下列问题: 、
、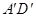 、
、 、
、 于
于 、
、 于
于 ,你认为
,你认为 的值(用含
的值(用含
 、
、 、
、 、
、 .小明在探究线段
.小明在探究线段 与
与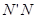 的数量关系时,从点
的数量关系时,从点 、
、 ,利用三角形全等、相似及锐角三角函数等相关知识解决了问题.请你参考小明的思路解答下列问题:
,利用三角形全等、相似及锐角三角函数等相关知识解决了问题.请你参考小明的思路解答下列问题: 、
、 、
、 、
、 于
于 、
、 于
于 ,你认为
,你认为 的值(用含
的值(用含