题目内容
(9分)我们把对称中心重合,四边分别平行的两个正方形之间的部分叫“方形环”,易知方形环四周的宽度相等.
一条直线l与方形环的边线有四个交点 、
、 、
、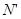 、
、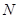 .小明在探究线段
.小明在探究线段 与
与 的数量关系时,从点
的数量关系时,从点 、
、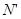 向对边作垂线段
向对边作垂线段 、
、 ,利用三角形全等、相似及锐角三角函数等相关知识解决了问题.请你参考小明的思路解答下列问题:
,利用三角形全等、相似及锐角三角函数等相关知识解决了问题.请你参考小明的思路解答下列问题:
⑴当直线l与方形环的对边相交时(如图1),直线l分别交 、
、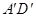 、
、 、
、 于
于 、
、 、
、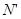 、
、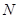 ,小明发现
,小明发现 与
与 相等,请你帮他说明理由;
相等,请你帮他说明理由;
⑵当直线l与方形环的邻边相交时(如图2),l分别交 、
、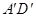 、
、 、
、 于
于 、
、 、
、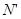 、
、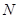 ,l与
,l与 的夹角为
的夹角为 ,你认为
,你认为 与
与 还相等吗?若 相等,说明理由;若不相等,求出
还相等吗?若 相等,说明理由;若不相等,求出 的值(用含
的值(用含 的三角函数表示).
的三角函数表示).
⑴解: 在方形环中,
∵ ∥
∥
∴
∴△ ≌△
≌△
∴ ·········· 3分
·········· 3分
⑵解法一:∵
∴ ∽
∽
∴
∵
∴ (或
(或 )
)
①当 时,tan
时,tan =1,则
=1,则
②当 时,
时,
则  (或
(或 )
)
解法二:在方形环中,
又∵
∴ ∥
∥
∴
在 与
与 中,
中,


即  (或
(或 )
)
①当 时,
时,
②当 时,
时,
则  (或
(或 ) ………………9分
) ………………9分
解析

练习册系列答案
相关题目
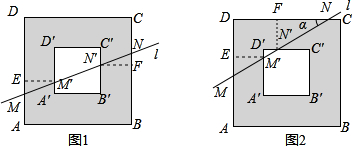
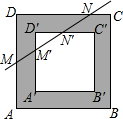 我们把对称中心重合,四边分别平行的两个正方形之间的部分叫“方形环”,已知方形环四周的宽度相等,如图,若直线l分别交方形环的邻边AD、A'D'、D'C'、DC于点M、M'、N'、N,且M为AD的中点,DN=3CN,则线段MM'与NN'的长度之比为
我们把对称中心重合,四边分别平行的两个正方形之间的部分叫“方形环”,已知方形环四周的宽度相等,如图,若直线l分别交方形环的邻边AD、A'D'、D'C'、DC于点M、M'、N'、N,且M为AD的中点,DN=3CN,则线段MM'与NN'的长度之比为
 、
、 、
、 、
、 .小明在探究线段
.小明在探究线段 与
与 的数量关系时,从点
的数量关系时,从点 、
、 ,利用三角形全等、相似及锐角三角函数等相关知识解决了问题.请你参考小明的思路解答下列问题:
,利用三角形全等、相似及锐角三角函数等相关知识解决了问题.请你参考小明的思路解答下列问题: 、
、 、
、 、
、 于
于 、
、 于
于 ,你认为
,你认为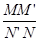 的值(用含
的值(用含
 、
、 、
、 、
、 .小明在探究线段
.小明在探究线段 与
与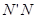 的数量关系时,从点
的数量关系时,从点 、
、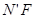 ,利用三角形全等、相似及锐角三角函数等相关知识解决了问题.请你参考小明的思路解答下列问题:
,利用三角形全等、相似及锐角三角函数等相关知识解决了问题.请你参考小明的思路解答下列问题: 、
、 、
、 、
、 于
于 、
、 于
于 ,你认为
,你认为 的值(用含
的值(用含