题目内容
19.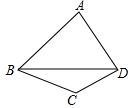 如图四边形ABCD中,∠ABC=3∠CBD,∠ADC=3∠CDB,∠C=128°,则∠A的度数是( )
如图四边形ABCD中,∠ABC=3∠CBD,∠ADC=3∠CDB,∠C=128°,则∠A的度数是( )| A. | 60° | B. | 76° | C. | 77° | D. | 78° |
分析 先设∠CBD=x°,∠CDB=y°,根据三角形的内角和整体得:x+y=52,则3x+3y=156,利用四边形的内角和可以求出∠A的度数.
解答 解:设∠CBD=x°,∠CDB=y°,则∠ABC=3x°,∠ADC=3y°,
∵∠C=128°,
∴∠CBD+∠CDB=180°-∠C=180°-128°=52°,
即x+y=52,
∴3x+3y=3×52=156,
∴∠ABC+∠ADC=156°,
∵∠A+∠ABC+∠ADC+∠C=360°,
∴∠A=360°-156°-128°=76°,
故选B.
点评 本题属于基础题,比较简单,考查了多边形的内角和,要熟练掌握三角形的内角和为180°,四边形的内角和为360°,本题还运用了整体的思想,这在数学解题中经常运用,要熟练掌握.

练习册系列答案
相关题目
7.下列各数中,既是分数又是负数的是( )
| A. | -3.1 | B. | 6 | C. | 0 | D. | 2.8 |
4.二次函数y=x2+mx+1的图象的顶点在坐标轴上,则m的值( )
| A. | 0 | B. | 2 | C. | ±2 | D. | 0或±2 |
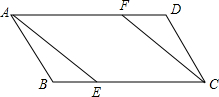 如图,在?ABCD中,点E、F分别在边BC和AD上,且BE=DF.求证:AE=CF.
如图,在?ABCD中,点E、F分别在边BC和AD上,且BE=DF.求证:AE=CF.