题目内容
如图,已知等腰Rt△AOB,其中∠AOB=90°,OA=OB=2,E、F为斜边AB上的两个动点(E比F更靠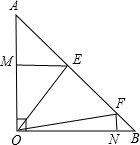 近A),满足∠EOF=45°,
近A),满足∠EOF=45°,
(1)求证:△AOF∽△BEO;
(2)求AF•BE的值;
(3)作EM⊥OA于M,FN⊥OB于N,求OM•ON的值;
(4)求线段EF长的最小值.(提示:必要时可以参考以下公式:当x>0,y>0时,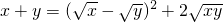 或
或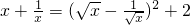 )
)
(1)证明:∵△AOB是等腰直角三角形,
∴∠A=∠B=45°.
∵∠AFO=∠B+∠BOF=45°+∠BOF,
又∵∠BOE=∠EOF+∠BOF=45°+∠BOF,
∴∠AFO=∠BOE.
∴△AOF∽△BEO.
(2)∵△BOE∽△AOF,
∴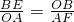 ,
,
∴AF•BE=4.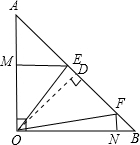
(3)作斜边AB上的高OD,并记OM=a,ON=b.
则易得ME=2-a,OD= ,FB=
,FB= BN=
BN= (2-b),
(2-b),
DF=BD-BF= -
- (2-b)=
(2-b)= (b-1),
(b-1),
∵∠EMO=∠ODF=90°,
∵∠EOF=45°,
∵∠MOE+∠EOD=∠FOD+∠EOD=45°
∴∠MOE=∠DOF,
∴△MOE∽△DOF,
∴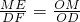 ,
,
∴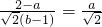 ,
,
∴ab=2,
即OM•ON=2.
(4)解: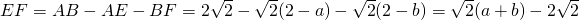 =
=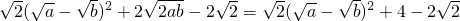 ,
,
所以,当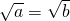 ,
, 时,EF取得最小值
时,EF取得最小值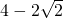 .
.
分析:(1)根据等腰直角三角形的性质,得∠A=∠B=45°;根据三角形的外角的性质,得∠AFO=∠B+∠BOF=45°+∠BOF,结合∠BOE=∠EOF+∠BOF=45°+∠BOF,证明∠AFO=∠BOE,从而根据两角对应相等,即可证明△AOF∽△BEO;
(2)根据相似三角形的性质,得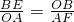 ,即AF•BE=4;
,即AF•BE=4;
(3)作斜边AB上的高OD,并记OM=a,ON=b.根据等腰直角三角形的性质,可以分别用a表示ME,DF,BN的长;根据△MOE∽△DOF,就可求得OM•ON的值;
(4)用a和b表示EF的长,从而分析EF的最小值.
点评:此题综合考查了相似三角形的判定和性质、等腰直角三角形的性质以及函数的最小值的求法.
∴∠A=∠B=45°.
∵∠AFO=∠B+∠BOF=45°+∠BOF,
又∵∠BOE=∠EOF+∠BOF=45°+∠BOF,
∴∠AFO=∠BOE.
∴△AOF∽△BEO.
(2)∵△BOE∽△AOF,
∴
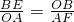 ,
,∴AF•BE=4.

(3)作斜边AB上的高OD,并记OM=a,ON=b.
则易得ME=2-a,OD=
 ,FB=
,FB= BN=
BN= (2-b),
(2-b),DF=BD-BF=
 -
- (2-b)=
(2-b)= (b-1),
(b-1),∵∠EMO=∠ODF=90°,
∵∠EOF=45°,
∵∠MOE+∠EOD=∠FOD+∠EOD=45°
∴∠MOE=∠DOF,
∴△MOE∽△DOF,
∴
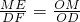 ,
,∴
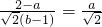 ,
,∴ab=2,
即OM•ON=2.
(4)解:
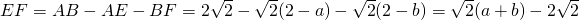 =
=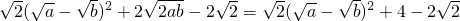 ,
,所以,当
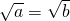 ,
, 时,EF取得最小值
时,EF取得最小值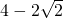 .
.分析:(1)根据等腰直角三角形的性质,得∠A=∠B=45°;根据三角形的外角的性质,得∠AFO=∠B+∠BOF=45°+∠BOF,结合∠BOE=∠EOF+∠BOF=45°+∠BOF,证明∠AFO=∠BOE,从而根据两角对应相等,即可证明△AOF∽△BEO;
(2)根据相似三角形的性质,得
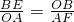 ,即AF•BE=4;
,即AF•BE=4;(3)作斜边AB上的高OD,并记OM=a,ON=b.根据等腰直角三角形的性质,可以分别用a表示ME,DF,BN的长;根据△MOE∽△DOF,就可求得OM•ON的值;
(4)用a和b表示EF的长,从而分析EF的最小值.
点评:此题综合考查了相似三角形的判定和性质、等腰直角三角形的性质以及函数的最小值的求法.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
 如图,已知等腰Rt△ABC,∠ACB=90°,AC=BC,D为BC边上一动点,BC=nDC,AD⊥EC于点E,延长BE交AC与点F.
如图,已知等腰Rt△ABC,∠ACB=90°,AC=BC,D为BC边上一动点,BC=nDC,AD⊥EC于点E,延长BE交AC与点F.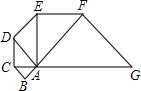 如图,已知等腰Rt△ABC的直角边长为l,以Rt△ABC的斜边AC为直角边,画第二个等腰Rt△ACD,再以Rt△ACD的斜边AD为直角边,画第三个等腰Rt△ADE,…,依此类推到第五个等腰Rt△AFG,则由这五个等腰直角三角形所构成的图形的面积为
如图,已知等腰Rt△ABC的直角边长为l,以Rt△ABC的斜边AC为直角边,画第二个等腰Rt△ACD,再以Rt△ACD的斜边AD为直角边,画第三个等腰Rt△ADE,…,依此类推到第五个等腰Rt△AFG,则由这五个等腰直角三角形所构成的图形的面积为 (2012•深圳二模)如图,已知等腰Rt△ABC中,∠B=90°,AB=BC=8cm,点P是线段AB上的点,点Q是线段BC延长线上的点,且AP=CQ,PQ与直线AC相交于点D.作PE⊥AC于点E,则线段DE的长度( )
(2012•深圳二模)如图,已知等腰Rt△ABC中,∠B=90°,AB=BC=8cm,点P是线段AB上的点,点Q是线段BC延长线上的点,且AP=CQ,PQ与直线AC相交于点D.作PE⊥AC于点E,则线段DE的长度( ) 如图,已知等腰Rt△ABC中,∠ACB=90°,AC=BC=4,D为△ABC的一个外角∠ABF的平分线上一点,且∠ADC=45°,CD交AB于E,
如图,已知等腰Rt△ABC中,∠ACB=90°,AC=BC=4,D为△ABC的一个外角∠ABF的平分线上一点,且∠ADC=45°,CD交AB于E, 如图,已知等腰Rt△ABC直角边长为1,以它的斜边AC为直角边画第二个等腰Rt△ACD,再以斜边AD为直角边画第三个Rt△ADE…,依此类推,AC长为
如图,已知等腰Rt△ABC直角边长为1,以它的斜边AC为直角边画第二个等腰Rt△ACD,再以斜边AD为直角边画第三个Rt△ADE…,依此类推,AC长为