题目内容
如图，已知等腰Rt△ABC，∠ACB=90°，AC=BC，D为BC边上一动点，BC=nDC，AD⊥EC于点E，延长BE交AC与点F．（1）若n=3，则
| CE |
| DE |
| AE |
| DE |
（2）若n=2，求证：AF=2FC；
（3）当n=
分析：（1）通过证明△CED∽△ACD，根据相似比即可求得CE：DE的长，同理可求得AE：DE的值．
（2）根据已知可求得△GED∽△AFE，根据相似比即可求得AF，FC的关系．
（3）要使AF=CF，必需n2=（n-1）：n．
（2）根据已知可求得△GED∽△AFE，根据相似比即可求得AF，FC的关系．
（3）要使AF=CF，必需n2=（n-1）：n．
解答：（1）由题意得，∠DEC=∠DCA=90°，∠EDC=∠CDA，
∴△CED∽△ACD．
∴CE：DE=AC：CD．
∵AC=BC，
∴AC：CD=n=3．
∴CE：DE=3．
同理可得：AE：DE=9．
（2）如图，当n=2时，D为BC的中点，取BF的中点G，连接DG，
则DG=
FC，DG∥FC．
∵CE⊥AD，∠ACB=90°，
∴∠ECD+∠EDC=∠CAD+∠ADC=90°．
∴∠ECD=∠CAD．
∵tan∠ECD=
，tan∠CAD=
=
，
∴
=
=
．
∵AC=BC，BC=2DC，
∴
=
=
=
．
∴
=
．
∵DG∥FA，
∴△GDE∽△FAE．
∴
=
．
∴DG=
AF．
∵DG=
FC，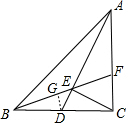
∴AF=2FC．
（3）如图，∵BC=nDC，
∴DC：BC=1：n，
∴DC：AC=1：n，
∴DE：CE：AE=1：n：n2；
∴DG：AF=1：n2；
又∵DG：CF=DB：BC=（BC-CD）：BC=（n-1）：n
要使AF=CF，必需n2=n：（n-1），（n＞0）
∴当n=
，F为AC的中点．
∴△CED∽△ACD．
∴CE：DE=AC：CD．
∵AC=BC，
∴AC：CD=n=3．
∴CE：DE=3．
同理可得：AE：DE=9．
（2）如图，当n=2时，D为BC的中点，取BF的中点G，连接DG，
则DG=
| 1 |
| 2 |
∵CE⊥AD，∠ACB=90°，
∴∠ECD+∠EDC=∠CAD+∠ADC=90°．
∴∠ECD=∠CAD．
∵tan∠ECD=
| ED |
| EC |
| DC |
| AC |
| EC |
| EA |
∴
| ED |
| EC |
| EC |
| EA |
| DC |
| AC |
∵AC=BC，BC=2DC，
∴
| ED |
| EC |
| EC |
| EA |
| DC |
| AC |
| 1 |
| 2 |
∴
| ED |
| AE |
| 1 |
| 4 |
∵DG∥FA，
∴△GDE∽△FAE．
∴
| DG |
| FA |
| DE |
| AE |
∴DG=
| 1 |
| 4 |
∵DG=
| 1 |
| 2 |
∴AF=2FC．
（3）如图，∵BC=nDC，
∴DC：BC=1：n，
∴DC：AC=1：n，
∴DE：CE：AE=1：n：n2；
∴DG：AF=1：n2；
又∵DG：CF=DB：BC=（BC-CD）：BC=（n-1）：n
要使AF=CF，必需n2=n：（n-1），（n＞0）
∴当n=
1+
| ||
| 2 |
点评：本题的关键是根据相似三角形得出线段之间的比例关系，进而得出所求线段与n之间的关系．
练习册系列答案
相关题目
如图，已知等腰Rt△ABC的直角边长为l，以Rt△ABC的斜边AC为直角边，画第二个等腰Rt△ACD，再以Rt△ACD的斜边AD为直角边，画第三个等腰Rt△ADE，…，依此类推到第五个等腰Rt△AFG，则由这五个等腰直角三角形所构成的图形的面积为
（2012•深圳二模）如图，已知等腰Rt△ABC中，∠B=90°，AB=BC=8cm，点P是线段AB上的点，点Q是线段BC延长线上的点，且AP=CQ，PQ与直线AC相交于点D．作PE⊥AC于点E，则线段DE的长度（ ）
如图，已知等腰Rt△ABC中，∠ACB=90°，AC=BC=4，D为△ABC的一个外角∠ABF的平分线上一点，且∠ADC=45°，CD交AB于E，
如图，已知等腰Rt△ABC直角边长为1，以它的斜边AC为直角边画第二个等腰Rt△ACD，再以斜边AD为直角边画第三个Rt△ADE…，依此类推，AC长为