题目内容
如图,已知直线 分别交
分别交 轴、
轴、 轴于A、B两点,抛物线
轴于A、B两点,抛物线 经过A、B两点,点C是抛物线与
经过A、B两点,点C是抛物线与 轴的另一个交点(与A点不重合)
轴的另一个交点(与A点不重合)

(1)求抛物线的解析式;
(2)求△ABC的面积;
(3)在抛物线的对称轴上,是否存在点M,使△ABM为等腰三角形?若不存在,请说明理由;若存在,求出点M的坐标。
(1) y=x2+2x-3.(2)6.(3)共存在4个点M1(-1, ),M2(-1,-
),M2(-1,- ),M3(-1,0),M4(-1,-1)使△ABM为等腰三角形.
),M3(-1,0),M4(-1,-1)使△ABM为等腰三角形.
【解析】
试题分析:(1)根据直线解析式求出点A及点B的坐标,然后将点A及点B的坐标代入抛物线解析式,可得出b、c的值,求出抛物线解析式;
(2)由(1)求得的抛物线解析式,可求出点C的坐标,继而求出AC的长度,代入三角形的面积公式即可计算;
(3)根据点M在抛物线对称轴上,可设点M的坐标为(-1,m),分三种情况讨论,①MA=BA,②MB=BA,③MB=MA,求出m的值后即可得出答案.
试题解析:(1)∵直线y=3x-3分别交x轴、y轴于A、B两点,
∴可得A(1,0),B(0,-3),
把A、B两点的坐标分别代入y=x2+bx+c得:
 ,
,
解得:b=2, c=-3.
∴抛物线解析式为:y=x2+2x-3.
(2)令y=0得:0=x2+2x-3,
解得:x1=1,x2=-3,
则C点坐标为:(-3,0),AC=4,
故可得S△ABC= AC×OB=
AC×OB= ×4×3=6.
×4×3=6.
(3)存在,理由如下:
抛物线的对称轴为:x=-1,假设存在M(-1,m)满足题意:
讨论:
①当MA=AB时,
∵OA=1,OB=3,
∴AB= ,
,
 ,
,
解得:m=± ,
,
∴M1(-1, ),M2(-1,-
),M2(-1,- );
);
②当MB=BA时, ,
,
解得:M3=0,M4=-6,
∴M3(-1,0),M4(-1,-6)(不合题意舍去),
③当MB=MA时, ,
,
解得:m=-1,
∴M5(-1,-1),
答:共存在4个点M1(-1, ),M2(-1,-
),M2(-1,- ),M3(-1,0),M4(-1,-1)使△ABM为等腰三角形.
),M3(-1,0),M4(-1,-1)使△ABM为等腰三角形.
考点:二次函数综合题.

八(2)班组织了一次经典朗读比赛,甲、乙两队各10人的比赛成绩如下表(10分制):
甲 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
乙 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(1)甲队成绩的中位数是 分,乙队成绩的众数是_____分;
(2)计算乙队的平均成绩和方差;
(3)已知甲队成绩的方差是1.4分2,则成绩较为整齐的是 队.
 ;
; .
. B.
B. C.
C. D.
D.

 轴对称的△A1B1C1。
轴对称的△A1B1C1。
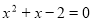 的解为
的解为 ,则
,则 =_____________ ,
=_____________ ,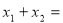 _____________
_____________ -3y+1)-3(2
-3y+1)-3(2