Question

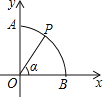
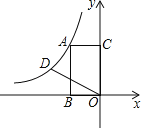
【题目】如图，矩形ABOC的顶点B、C分别在x轴，y轴上，顶点A在第二象限，点B的坐标为（﹣2，0）．将线段OC绕点O逆时针旋转60°至线段OD，若反比例函数y=（k≠0）的图象经过A、D两点，则k值为______．

Answer 1

【答案】.

【解析】

由B（﹣2，0）代入y=，用含有k的代数式表示出AB、OC，得到线段OD的长，再根据∠COD=60°，利用三角函数求出DE、OE，由此表示出点D的坐标，再将点D的坐标代入y=中即可求k的值.

如图，过点D作DE⊥x轴于点E，

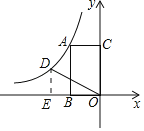
∵点B的坐标为（﹣2，0），

∴OB=2，

∴AB=﹣，∴OC=﹣，

由旋转性质知OD=OC=﹣，

∵∠COD=60°，

∴∠DOE=30°，

∴DE=OD=﹣k，OE=OD·cos30°=×（﹣）=﹣k，

即D（﹣k，﹣k），

∵反比例函数y=（k≠0）的图象经过D点，

∴k=（﹣k）（﹣k）=k2，

解得：k=0（舍）或k=﹣，

故答案为：﹣．