Question

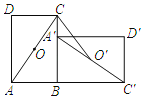
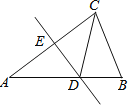
【题目】（2013年四川自贡12分）将两块全等的三角板如图①摆放，其中∠A1CB1=∠ACB=90°，∠A1=∠A=30°．

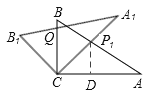
（1）将图①中的△A1B1C顺时针旋转45°得图②，点P1是A1C与AB的交点，点Q是A1B1与BC的交点，求证：CP1=CQ；

（2）在图②中，若AP1=2，则CQ等于多少？

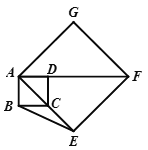
（3）如图③，在B1C上取一点E，连接BE、P1E，设BC=1，当BE⊥P1B时，求△P1BE面积的最大值．

Answer 1

【答案】解答：（1）证明：∵∠B1CB=45°，∠B1CA1=90°，∴∠B1CQ=∠BCP1=45°。

∵在△B1CQ和△BCP1中，，

∴△B1CQ≌△BCP1（ASA）。∴CQ=CP1。

（2）如图，过点P1作P1D⊥CA于D，

∵∠A=30°，∴P1D=AP1=1。

∵∠P1CD=45°，∴。.

∴CP1=P1D=。

又∵CP1=CQ，∴CQ=。

（3）∵∠P1BE=90°，∠ABC=60°，∴∠A=∠CBE=30°。∴AC=、BC 。

由旋转的性质可得：∠ACP1=∠BCE，∴△AP1C∽△BEC。∴AP1：BE=AC：BC=：1。

设AP1=x，则BE=x，

在Rt△ABC中，∠A=30°，∴AB=2BC=2。

∴。

∵，∴当x=1时，S△P1BE（max）=。

【解析】（1）先判断∠B1CQ=∠BCP1=45°，利用ASA即可证明△B1CQ≌△BCP1，从而得出结论。

（2）过点P1作P1D⊥CA于D，在RtADP1中，求出P1D，在Rt△CDP1中求出CP1，继而可得出CQ的长度。

（3）证明△AP1C∽△BEC，则有AP1：BE=AC：BC=：1，设AP1=x，则BE=x，得出S△P1BE关于x的表达式，利用配方法求最值即可。