题目内容
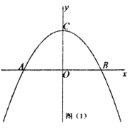
【题目】如图,抛物线![]() 交
交![]() 轴于
轴于![]() 、
、![]() (
(![]() 左
左![]() 右)两点,交
右)两点,交![]() 轴于点
轴于点![]() ,且
,且![]() .
.
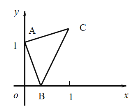
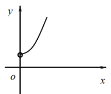
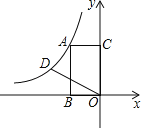
(1)如图(1)求抛物线的解析式;
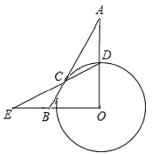
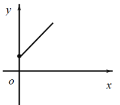
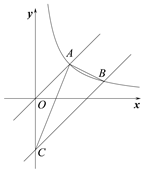
(2)如图(2)![]() 为第四象限抛物线上一点,连接
为第四象限抛物线上一点,连接![]() ,将线段
,将线段![]() 沿着
沿着![]() 轴翻折,得到线段
轴翻折,得到线段![]() ,连接
,连接![]() ,设
,设![]() 点的横坐标为
点的横坐标为![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 的函数关系式;
的函数关系式;
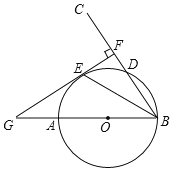
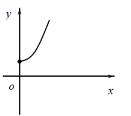
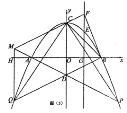
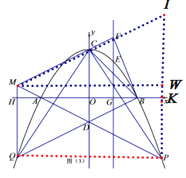
(3)如图(3)在(2)的条件下,![]() 是第一象限抛物线上的一点,
是第一象限抛物线上的一点,![]() 轴交
轴交![]() 的延长线于
的延长线于![]() ,垂足是
,垂足是![]() ,过点
,过点![]() 作
作![]() 轴交
轴交![]() 轴于
轴于![]() 、交直线
、交直线![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() ,求点
,求点![]() 的坐标.
的坐标.

【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)当x=0时, y=c,则C(0,c)、B(c,0)、A(-c,0),将点A、B的坐标代入二次函数表达式,即可求解;
(2)利用S△BCQ=![]() ·CD·(OB+OH)即可求解;
·CD·(OB+OH)即可求解;
(3)证明MI=MP,CD=MQ,而由(2)知:CD=m,CD=![]() PI,PI=2m,则IW=WP=m,由tan∠WMP=
PI,PI=2m,则IW=WP=m,由tan∠WMP=![]() 得tana=
得tana=![]() ,而
,而![]() 可得
可得 ,由此可求解.
,由此可求解.
解:(1)当x=0时,y=c,
∴C(0,c),
∴OC=c
∵OA=OB=OC
∴B(c,0),A(-c,0)
代入解析式得:b=0,c=4或0(0不符合题意舍去)
∴抛物线的解析式为:![]()
(2)∵点P在抛物线上,
则![]()
∵P、Q关于y轴对称,
![]()
作OH⊥x轴于H,tan∠ABO=tan∠OBD,
则OD=m-4,OC=4,CD=m,
S△BCQ=![]() ·CD·(OB+OH)=
·CD·(OB+OH)= ![]() m+2m,
m+2m,
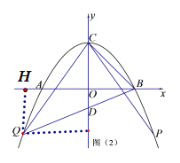
(3)过点P作PK⊥x轴于点K,与MF的延长线交于点I,连接PQ,
设∠BAP=a,则∠APK=90°-a,
∵∠PMF=2∠BAP=2a,∠I=90°-a,
∴MI=MP,
过M作MW⊥IP于点W,则MQPW是矩形
∵CD∥QM,CD=WP=QM
∴CD=QM
由(2)知:CD=m,
∵CD∥PI,
∴CD=![]() PI,PI=2m
PI,PI=2m
∴IW=WP=m
∴∠WMP=∠BAP=a
∴tan∠WMP=PW∶WM=![]() ,
,
∴tana=![]() ,
,
∵![]() ,
,
∴ ,
,
解得:![]() 或4(舍去4)
或4(舍去4)
∴点P(6,-5)

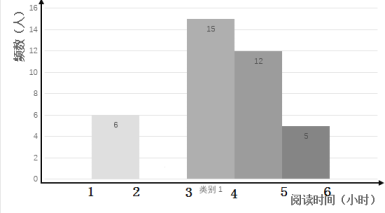
【题目】在开展“经典阅读”活动中,某学校为了解全校学生利用课外时间阅读的情况,学校团委随机抽取若干名学生,调查他们一周的课外阅读时间,并根据调查结果绘制了如下尚不完整的统计表.根据图表信息,解答下列问题:
频率分布表
阅读时间(小时) | 频数(人) | 频率 |
| 6 | 0.12 |
|
| 0.24 |
| 15 | 0.3 |
| 12 |
|
| 5 | 0.1 |
合计 |
| 1 |
(1)求![]() __________,
__________,![]() _________;
_________;
(2)将频数分布直方图补充完整(画图后请标注相应的频数);
(3)在![]() 范围内的5名同学中恰好有2名男生和3名女生,现从中随机挑选2名同学代表学校参加全市经典阅读比赛,请用树状图法或者列表法求出恰好选中“1男1女”的概率.
范围内的5名同学中恰好有2名男生和3名女生,现从中随机挑选2名同学代表学校参加全市经典阅读比赛,请用树状图法或者列表法求出恰好选中“1男1女”的概率.