题目内容
一个正三角形的边长为4，则一边上的高为分析：根据等边三角形三线合一的性质，即可得D为BC的中点，即可求BD的值，已知AB、BD根据勾股定理即可求AD的值．
解答：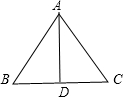
解：∵等边三角形三线合一，
∴D为BC的中点，
∴BD=
BC=2，
在Rt△ABD中，AB=4，BD=2，
则AD=
=2
．
故答案为：2
．
解：∵等边三角形三线合一，∴D为BC的中点，
∴BD=
| 1 |
| 2 |
在Rt△ABD中，AB=4，BD=2，
则AD=
| AB2-BD2 |
| 3 |
故答案为：2
| 3 |
点评：本题考查了勾股定理在直角三角形中的运用，等边三角形三线合一的性质，本题中根据勾股定理求AD的值是解题的关键．
练习册系列答案
相关题目
如图，用两段等长的铁丝恰好可以分别围成一个正三角形和一个正方形，其中正三角形的边长为（x2+15）cm，正方边形的边长为（x2+x）cm（其中x＞0）．则这两段铁丝的总长是
