题目内容
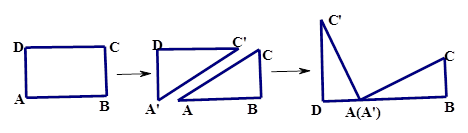
将矩形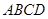 纸片沿对角线
纸片沿对角线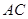 剪开,得
剪开,得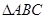 和
和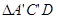 ,如图(1-1)所示.将
,如图(1-1)所示.将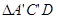 的顶点
的顶点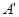 与点
与点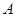 重合,并绕点
重合,并绕点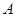 按逆时针方向旋转,使点
按逆时针方向旋转,使点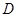 、
、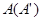 、
、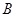 在同一条直线上,如图(1-2)所示.
在同一条直线上,如图(1-2)所示.
小题1:观察图可知:与BC相等的线段是______,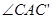 =_______;
=_______;
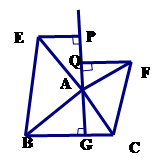
小题2:如图(2), 中,
中, 于点
于点 ,以
,以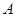 为直角顶点,分别以
为直角顶点,分别以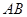 、
、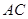 为直角边,向
为直角边,向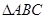 外作等腰
外作等腰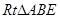 和等腰
和等腰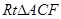 ,过点
,过点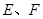 作射线
作射线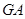 的垂线,垂足分别为
的垂线,垂足分别为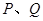 . 求证:
. 求证: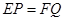 .
.
小题3:如图(3), 中,
中,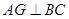 于点
于点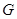 ,以
,以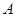 为直角顶点,分别以
为直角顶点,分别以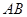 、
、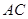 为直角边,向
为直角边,向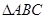 外作
外作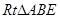 和
和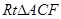 ,过点
,过点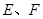 作射线
作射线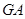 的垂线,垂足分别为
的垂线,垂足分别为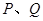 .若
.若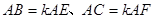 ,试探究
,试探究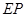 与
与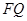 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.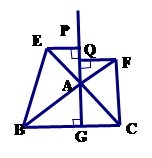
 纸片沿对角线
纸片沿对角线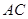 剪开,得
剪开,得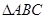 和
和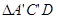 ,如图(1-1)所示.将
,如图(1-1)所示.将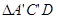 的顶点
的顶点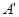 与点
与点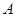 重合,并绕点
重合,并绕点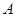 按逆时针方向旋转,使点
按逆时针方向旋转,使点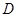 、
、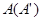 、
、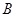 在同一条直线上,如图(1-2)所示.
在同一条直线上,如图(1-2)所示.小题1:观察图可知:与BC相等的线段是______,
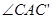 =_______;
=_______;
小题2:如图(2),
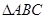 中,
中,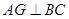 于点
于点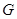 ,以
,以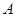 为直角顶点,分别以
为直角顶点,分别以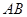 、
、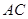 为直角边,向
为直角边,向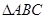 外作等腰
外作等腰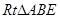 和等腰
和等腰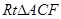 ,过点
,过点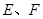 作射线
作射线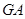 的垂线,垂足分别为
的垂线,垂足分别为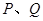 . 求证:
. 求证: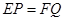 .
.
小题3:如图(3),
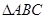 中,
中,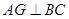 于点
于点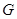 ,以
,以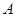 为直角顶点,分别以
为直角顶点,分别以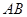 、
、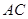 为直角边,向
为直角边,向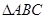 外作
外作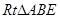 和
和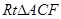 ,过点
,过点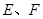 作射线
作射线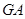 的垂线,垂足分别为
的垂线,垂足分别为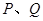 .若
.若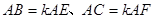 ,试探究
,试探究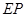 与
与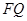 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
小题1:AD(
 )……2分
)……2分  ………4分
………4分小题2:

EP=AG………6分

FQ=AG
EP=FQ……………………………8分
小题3:
 ~
~
 ………………10分
………………10分 ~
~

EP=FQ……………………………12分
(1)根据将矩形ABCD纸片沿对角线AC剪开,得到△ABC和△A′C′D,利用矩形性质即可得出与BC相等的线段以及∠CAC′的度数;
(2)根据全等三角形的判定得出△ABG≌△EAP,进而求出AG=EP.同理AG=FQ,即EP="FQ;"
(3)根据相似三角形的判定得出 ~
~ ,进而求出
,进而求出 ,同理可求出
,同理可求出 ,即EP=FQ.
,即EP=FQ.
(2)根据全等三角形的判定得出△ABG≌△EAP,进而求出AG=EP.同理AG=FQ,即EP="FQ;"
(3)根据相似三角形的判定得出
 ~
~ ,进而求出
,进而求出 ,同理可求出
,同理可求出 ,即EP=FQ.
,即EP=FQ.
练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
 b,得a2-b2=(
b,得a2-b2=(

 ,其中较小多边形周长为36cm,则较大多边形周长为
,其中较小多边形周长为36cm,则较大多边形周长为
 中,BC边在x轴上,点A(-1,2),点C(3,0) .动点P从点A出发,以每秒1个单位的速度沿AD向点D运动,到达点D后停止.把BP的中点M绕点P逆时针旋转90°到点N,连接PN,DN.设P的运动时间为t秒.
中,BC边在x轴上,点A(-1,2),点C(3,0) .动点P从点A出发,以每秒1个单位的速度沿AD向点D运动,到达点D后停止.把BP的中点M绕点P逆时针旋转90°到点N,连接PN,DN.设P的运动时间为t秒.