题目内容
如图，P为⊙O外一点，PA切⊙O于点A，且OP=5，PA=4，则sin∠APO等于
- A.
- B.
- C.
- D.
B
分析：连接OA，由勾股定理得OA=3，从而得sin∠APO=．
解答：
解：连接OA，
由切线性质知，∠PAO=90°．
在Rt△PAO中，OP=5，PA=4，由勾股定理得OA=3．
∴sin∠APO=．
故选B．
点评：本题可以考查锐角三角函数的定义：在直角三角形中，锐角的正弦为对边比斜边，余弦为邻边比斜边，正切为对边比邻边．
分析：连接OA，由勾股定理得OA=3，从而得sin∠APO=
．解答：
解：连接OA，由切线性质知，∠PAO=90°．
在Rt△PAO中，OP=5，PA=4，由勾股定理得OA=3．
∴sin∠APO=
．故选B．
点评：本题可以考查锐角三角函数的定义：在直角三角形中，锐角的正弦为对边比斜边，余弦为邻边比斜边，正切为对边比邻边．
练习册系列答案
相关题目
10、如图，P为⊙O外一点，PA、PB分别切⊙O于A、B，CD切⊙O于点E，分别交PA、PB于点C、D，若PA=5，则△PCD的周长为（ ）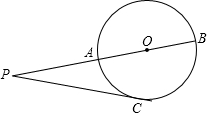
已知如图，P为⊙O外一点，过点P作⊙O的切线，切点为C，过P，O两点作⊙O的割线交⊙O于A、B两点，且PC=4cm，PA=3cm，则⊙O的半径R=
如图，P为圆外一点，PA切圆于A，PA=8，直线PCB交圆于C、B，且PC=4，连接AB、AC，∠ABC=α，∠ACB=β，则
如图，P为⊙O外一点，PA切⊙O于点A，且OP=5，PA=4，则sin∠APO=
如图，P为⊙O外一点，过点P作⊙O的两条割线，分别交⊙O于A、B和C、D，且AB为⊙O的直径，已知PA=AO=2cm，弧AC=弧CD，则PC的长为（ ）