题目内容
如图，P为⊙O外一点，过点P作⊙O的两条割线，分别交⊙O于A、B和C、D，且AB为⊙O的直径，已知PA=AO=2cm，弧AC=弧CD，则PC的长为（ ）分析：根据已知可得出OC∥BD，根据平行线分线段成比例可得到关于PC，PD的关系式，再结合切割线定理的推论，也可得出关于PC，PD的关系式，联合起来，解方程就可分别求出PC．
解答：
解：连接OC、OD．
∵弧AC=弧CD，
∴∠AOC=COD=
∠AOD；
又∵∠ABD=
∠AOD，
∴∠ABD=∠AOC，
∴OC∥BD，
∴
=
，
∴
=
=
，
∴PD=
PC；
∵PD和PB都是⊙O外同一点引出的割线，
∴PC•PD=PA•PB，
∴PC•PD=2×6=12，
∴PC=2
cm．
故选D．
解：连接OC、OD．∵弧AC=弧CD，
∴∠AOC=COD=
| 1 |
| 2 |
又∵∠ABD=
| 1 |
| 2 |
∴∠ABD=∠AOC，
∴OC∥BD，
∴
| PC |
| PD |
| PO |
| PB |
∴
| PC |
| PD |
| 4 |
| 6 |
| 2 |
| 3 |
∴PD=
| 3 |
| 2 |
∵PD和PB都是⊙O外同一点引出的割线，
∴PC•PD=PA•PB，
∴PC•PD=2×6=12，
∴PC=2
| 2 |
故选D．
点评：本题利用了圆周角定理，以及平行线分线段成比例定理，切割线定理的推论等知识．
练习册系列答案
相关题目
10、如图，P为⊙O外一点，PA、PB分别切⊙O于A、B，CD切⊙O于点E，分别交PA、PB于点C、D，若PA=5，则△PCD的周长为（ ）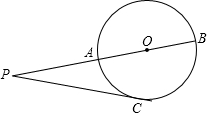
已知如图，P为⊙O外一点，过点P作⊙O的切线，切点为C，过P，O两点作⊙O的割线交⊙O于A、B两点，且PC=4cm，PA=3cm，则⊙O的半径R=
如图，P为圆外一点，PA切圆于A，PA=8，直线PCB交圆于C、B，且PC=4，连接AB、AC，∠ABC=α，∠ACB=β，则
如图，P为⊙O外一点，PA切⊙O于点A，且OP=5，PA=4，则sin∠APO=