题目内容
15. “马航失联飞机”牵动世界各国人民的心,许多国家积极组织船只进行搜救.如图,某搜救船在A处望见一可疑物P在北偏东60°方向,同时另一搜救船在B处望见可疑物P在北偏西45°方向.已知AB两处相距800海里,求B处离可疑物P的距离.(结果保留根号)
“马航失联飞机”牵动世界各国人民的心,许多国家积极组织船只进行搜救.如图,某搜救船在A处望见一可疑物P在北偏东60°方向,同时另一搜救船在B处望见可疑物P在北偏西45°方向.已知AB两处相距800海里,求B处离可疑物P的距离.(结果保留根号)
分析 作PC⊥AB于C点,设PC=x,解直角三角形APC求的AC,解直角三角形BPC求得BC和PB,然后根据题意得出关于x的方程,即方程求得x的值,即可求得PB的长.
解答 解:作PC⊥AB于C点,设PC=x,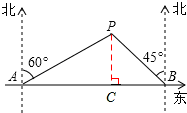
∵∠PAB=30°,∠PBA=45°.
∴BC=x,PB=$\sqrt{2}$x,AC=$\sqrt{3}$x.
∵AB=800,
∴$\sqrt{3}$x+x=800,
解得x=400($\sqrt{3}$-1),
∴PB=400($\sqrt{6}-\sqrt{2}$)(海里).
点评 本题主要考查了利用三角函数解直角三角形,把一般三角形通过作高线转化为直角三角形是解题的关键.

练习册系列答案
 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
3.云南省鲁甸县2014年8月3日发生6.5级地震,造成重大人员伤亡和经济损失.灾情牵动亿万同胞的心,在灾区人民最需要援助的时刻,全国同胞充分发扬“一方有难、八方支援”的中华民族优良传统,及时向灾区同胞伸出援助之手.截至9月19日17时,云南省级共接收昭通鲁甸“8.3”地震捐款80100万元.科学记数法表示为( )元.
| A. | 8.01×107 | B. | 80.1×107 | C. | 8.01×108 | D. | 0.801×109 |
5.一组数据如下:3,6,7,2,3,4,3,6,那么这组数据的中位数和众数分别是( )
| A. | 3,3 | B. | 3.5,3 | C. | 4,3 | D. | 3.5,6 |
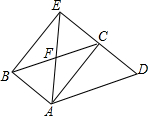 如图,在平行四边形ABCD中,AB=$\sqrt{3}$,AC=3,过点B作BE平行AC交DC的延长线于点E,连结AE,AE交BC于点F,若AB⊥AC,求△ADE的周长.
如图,在平行四边形ABCD中,AB=$\sqrt{3}$,AC=3,过点B作BE平行AC交DC的延长线于点E,连结AE,AE交BC于点F,若AB⊥AC,求△ADE的周长.