题目内容
10.函数y=$\sqrt{2-x}$+$\frac{1}{x}$中,自变量x的取值范围是x≤2且x≠0.分析 根据二次根式的性质和分式的意义,被开方数大于或等于0,分母不等于0,可以求出x的范围.
解答 解:根据题意得:2-x≥0且x≠0,
解得:x≤2且x≠0.
故答案为x≤2且x≠0.
点评 本题考查了函数自变量的取值范围问题,函数自变量的范围一般从三个方面考虑:
(1)当函数表达式是整式时,自变量可取全体实数;
(2)当函数表达式是分式时,考虑分式的分母不能为0;
(3)当函数表达式是二次根式时,被开方数非负.

练习册系列答案
相关题目
5.下列各式中正确的是( )
| A. | 3-2=-9 | B. | (72)3=75 | C. | x10÷x5=x2 | D. | $\frac{1}{\sqrt{2}-1}$=$\sqrt{2}$+1 |
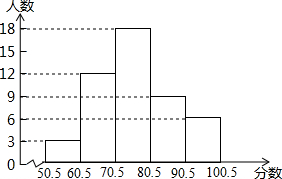 某校一次知识竞赛,竞赛成绩(取整数),进行整理后分五组,并绘制成频数分布直方图,结合图形,解答下列问题:
某校一次知识竞赛,竞赛成绩(取整数),进行整理后分五组,并绘制成频数分布直方图,结合图形,解答下列问题: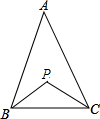 如图,在△ABC中,BP、CP分别为∠B、∠C的平分线,请探究∠A和∠P之间存在怎样的数量关系?说说你的理由.
如图,在△ABC中,BP、CP分别为∠B、∠C的平分线,请探究∠A和∠P之间存在怎样的数量关系?说说你的理由.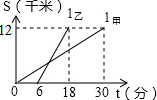 甲、乙两人前往12千米外的地方植树.图中l甲、l乙分别表示甲、乙行驶的路程S(千米)与时间t(分)的函数关系,则每分钟乙比甲多走$\frac{3}{5}$千米.
甲、乙两人前往12千米外的地方植树.图中l甲、l乙分别表示甲、乙行驶的路程S(千米)与时间t(分)的函数关系,则每分钟乙比甲多走$\frac{3}{5}$千米.