ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩ‘ΡΕΝœ¬ΟφΒΡάΐΧβΦΑΒψ≤ΠΘ§≤Ι»ΪΫβΧβΙΐ≥ΧΘ®Άξ≥…Βψ≤Π≤ΩΖ÷ΒΡΧνΩ’Θ©Θ§≤ΔΫβΨωΈ ΧβΘΚ
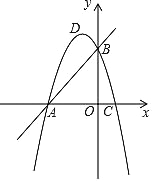
άΐΧβΘΚ»γΆΦ1Θ§‘ΎΒ»±Ώ![]() ÷–Θ§
÷–Θ§![]() «
«![]() ±Ώ…œ“ΜΒψΘ®≤ΜΚ§ΕΥΒψ
±Ώ…œ“ΜΒψΘ®≤ΜΚ§ΕΥΒψ![]() Θ©Θ§
Θ©Θ§![]() «
«![]() ΒΡΆβΫ«
ΒΡΆβΫ«![]() ΒΡΤΫΖ÷œΏ…œ“ΜΒψΘ§«“
ΒΡΤΫΖ÷œΏ…œ“ΜΒψΘ§«“![]() .«σ÷ΛΘΚ
.«σ÷ΛΘΚ![]() Θ°
Θ°
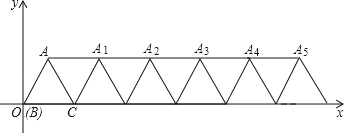
 ΓΓΓΓΓΓ
ΓΓΓΓΓΓ ΓΓΓΓΓΓ
ΓΓΓΓΓΓ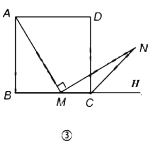
Βψ≤ΠΘΚ»γΆΦ2Θ§Ής![]() Θ§
Θ§![]() ”κ
”κ![]() ΒΡ―”≥ΛœΏœύΫΜ”ΎΒψ
ΒΡ―”≥ΛœΏœύΫΜ”ΎΒψ![]() Θ§ΒΟΒ»±Ώ
Θ§ΒΟΒ»±Ώ![]() Θ§Ν§Ϋα
Θ§Ν§Ϋα![]() Θ§“Ή÷Λ
Θ§“Ή÷Λ![]() Θ®_______Θ©Θ§Ω…ΒΟ
Θ®_______Θ©Θ§Ω…ΒΟ![]() Θ§
Θ§![]() ΘΜ
ΘΜ
”÷![]() Θ§‘ρ
Θ§‘ρ![]() Θ§Ω…ΒΟ
Θ§Ω…ΒΟ![]() ____
____![]() _____ΘΜ
_____ΘΜ
”…![]() Θ§Ϋχ“Μ≤ΫΩ…ΒΟ
Θ§Ϋχ“Μ≤ΫΩ…ΒΟ![]() ______ΘΜ
______ΘΜ
”÷“ρΈΣ![]() Θ§Υυ“‘
Θ§Υυ“‘![]() Θ§Υυ“‘
Θ§Υυ“‘![]() Θ°
Θ°
Έ ΧβΘΚ»γΆΦ3Θ§ΥΡ±Ώ–Έ![]() ΒΡΥΡΧθ±ΏΕΦœύΒ»Θ§ΥΡΗωΫ«ΕΦΒ»”Ύ
ΒΡΥΡΧθ±ΏΕΦœύΒ»Θ§ΥΡΗωΫ«ΕΦΒ»”Ύ![]() Θ§
Θ§![]() «
«![]() ±Ώ…œ“ΜΒψΘ®≤ΜΚ§ΕΥΒψ
±Ώ…œ“ΜΒψΘ®≤ΜΚ§ΕΥΒψ![]() Θ©Θ§
Θ©Θ§![]() «ΥΡ±Ώ–Έ
«ΥΡ±Ώ–Έ![]() ΒΡΆβΫ«
ΒΡΆβΫ«![]() ΒΡΤΫΖ÷œΏ…œ“ΜΒψΘ§«“
ΒΡΤΫΖ÷œΏ…œ“ΜΒψΘ§«“![]() Θ°«σ
Θ°«σ![]() ΒΡΕ» ΐΘ°
ΒΡΕ» ΐΘ°
ΓΨ¥πΑΗΓΩΒψ≤ΠΘΚ![]() ΘΜ
ΘΜ![]() ΓΓ
ΓΓ![]() ΘΜ
ΘΜ![]() ΘΜΈ ΧβΘΚ
ΘΜΈ ΧβΘΚ![]() Θ°
Θ°
ΓΨΫβΈωΓΩ
Βψ≤ΠΘΚ”…SASΩ…ΒΟΘΚ![]() Θ§ΗυΨίΒ»―ϋΒΡ–‘÷ Ω…ΒΟ
Θ§ΗυΨίΒ»―ϋΒΡ–‘÷ Ω…ΒΟ![]() Θ§”…
Θ§”…![]() Θ§Ω…ΒΟΘΚ
Θ§Ω…ΒΟΘΚ![]() ΘΜ
ΘΜ
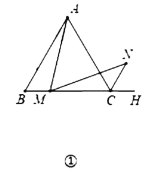
Έ ΧβΘΚΉς![]() Θ§
Θ§![]() ”κ
”κ![]() Ζ¥œρ―”≥ΛœΏΫΜ”Ύ
Ζ¥œρ―”≥ΛœΏΫΜ”Ύ![]() Θ§ΒΟΒ»―ϋ÷±Ϋ«»ΐΫ«–Έ
Θ§ΒΟΒ»―ϋ÷±Ϋ«»ΐΫ«–Έ![]() Θ§Ν§Ϋ”
Θ§Ν§Ϋ”![]() Θ§”…SASΩ…÷Λ
Θ§”…SASΩ…÷Λ![]() Θ§ΒΟ≥ωAM=MGΘ§Γœ1=Γœ2Θ§ΒΟ≥ωMG=MNΘ§”…Β»―ϋ»ΐΫ«–ΈΒΡ–‘÷ ΒΟ≥ωΓœ3=Γœ4Θ§÷Λ≥ωΓœ1=Γœ2=Γœ5Θ§ΒΟ≥ωΓœ5+Γœ6=90ΓψΘ§Φ¥Ω…ΒΟ≥ωΫα¬έΘ°
Θ§ΒΟ≥ωAM=MGΘ§Γœ1=Γœ2Θ§ΒΟ≥ωMG=MNΘ§”…Β»―ϋ»ΐΫ«–ΈΒΡ–‘÷ ΒΟ≥ωΓœ3=Γœ4Θ§÷Λ≥ωΓœ1=Γœ2=Γœ5Θ§ΒΟ≥ωΓœ5+Γœ6=90ΓψΘ§Φ¥Ω…ΒΟ≥ωΫα¬έΘ°
Βψ≤ΠΘΚ![]() ΒΡΧθΦΰΈΣ:
ΒΡΧθΦΰΈΣ:
![]()
![]()
![]() .
.
Ι »ΪΒ»ΧθΦΰΈΣ![]()
”…![]() Θ§Ι ”–
Θ§Ι ”–![]() .
.
”…”Ύ![]()
”÷ΓΏ![]()
Ι ![]() .
.
Ι ¥πΑΗΈΣΘΚ![]() ΘΜ
ΘΜ![]() ΓΓ
ΓΓ![]() ΘΜ
ΘΜ![]() ΘΜ
ΘΜ
Έ ΧβΘΚΉς![]() Θ§
Θ§![]() ”κ
”κ![]() Ζ¥œρ―”≥ΛœΏΫΜ”Ύ
Ζ¥œρ―”≥ΛœΏΫΜ”Ύ![]() Θ§ΒΟΒ»―ϋ÷±Ϋ«»ΐΫ«–Έ
Θ§ΒΟΒ»―ϋ÷±Ϋ«»ΐΫ«–Έ![]() Θ§Ν§Ϋ”
Θ§Ν§Ϋ”![]() Θ§
Θ§

‘Ύ’ΐΖΫ–Έ![]() ÷–Θ§
÷–Θ§![]()
”÷![]() Θ§Ι
Θ§Ι ![]() .
.
‘Ύ![]() ”κ
”κ![]() ÷–
÷–

Γύ![]() .
.
Γύ![]() ,
,![]()
”÷![]()
Γύ![]()
Γύ![]()
ΓΏ![]()
Γύ![]() .
.
Γύ![]()
Γύ![]()