题目内容
【题目】根据材料,解答问题
如图,数轴上有点![]() ,对应的数分别是6,-4,4,-1,则
,对应的数分别是6,-4,4,-1,则![]() 两点间的距离为
两点间的距离为![]() ;
;![]() 两点间的距离为
两点间的距离为![]() ;
;![]() 两点间的距离为
两点间的距离为![]() ;由此,若数轴上任意两点
;由此,若数轴上任意两点![]() 分别表示的数是
分别表示的数是![]() ,则
,则![]() 两点间的距离可表示为
两点间的距离可表示为![]() .反之,
.反之,![]() 表示有理数
表示有理数![]() 在数轴上的对应点
在数轴上的对应点![]() 之间的距离,称之为绝对值的几何意义.
之间的距离,称之为绝对值的几何意义.
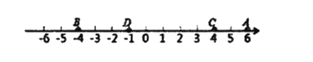
问题应用1:
(1)如果表示-1的点![]() 和表示
和表示![]() 的点
的点![]() 之间的距离是2,则点
之间的距离是2,则点![]() 对应的
对应的![]() 的值为___________;
的值为___________;
(2)方程![]() 的解
的解![]() ____________;
____________;
(3)方程![]() 的解
的解![]() ______________ ;
______________ ;
问题应用2:
如图,若数轴上表示![]() 的点为
的点为![]() .
.
(4)![]() 的几何意义是数轴上_____________,当
的几何意义是数轴上_____________,当![]() __________,
__________,![]() 的值最小是____________;
的值最小是____________;
(5)![]() 的几何意义是数轴上_______,
的几何意义是数轴上_______,![]() 的最小值是__________,此时点
的最小值是__________,此时点![]() 在数轴上应位于__________上;
在数轴上应位于__________上;
(6)根据以上推理方法可求![]() 的最小值是___________,此时
的最小值是___________,此时![]() __________.
__________.
【答案】(1)-3或1;(2)-7或1;(3)1;(4)点![]() 到4的距离;4;0;(5)点
到4的距离;4;0;(5)点![]() 到-1和到4的距离之和;5;线段CD;(6)2;2.
到-1和到4的距离之和;5;线段CD;(6)2;2.
【解析】
(1)根据数轴上两点间的距离的定义即可求解;
(2)根据数轴上两点间的距离的定义即可求解;
(3)根据数轴上两点间的距离的定义即可求解;
(4)绝对值的几何意义即可求解;
(5)绝对值的几何意义即可求解;
(6)绝对值的几何意义即可求解.
(1)如果表示-1的点![]() 和表示
和表示![]() 的点
的点![]() 之间的距离是2,则点
之间的距离是2,则点![]() 对应的
对应的![]() 的值为-3或1,
的值为-3或1,
故答案为:-3或1;
(2)![]() 即表示
即表示![]() 的点距离-3的点距离是4,则
的点距离-3的点距离是4,则![]() 的值为-7或1,
的值为-7或1,
故答案为:-7或1;
(3)![]() 即表示
即表示![]() 的点距离-4与6的距离相等,
的点距离-4与6的距离相等,
故m是-4与6的中点,
∴m=1;
故答案为:1;
(4)![]() 的几何意义是数轴上点
的几何意义是数轴上点![]() 到4的距离,当
到4的距离,当![]() 4,
4,![]() 的值最小是0
的值最小是0
故答案为:点![]() 到4的距离;4;0;
到4的距离;4;0;
(5)![]() 的几何意义是数轴上点
的几何意义是数轴上点![]() 到-1和到4的距离之和,
到-1和到4的距离之和,![]() 的最小值是5,此时点
的最小值是5,此时点![]() 在数轴上应位于线段CD上
在数轴上应位于线段CD上
故答案为:点![]() 到-1和到4的距离之和;5;线段CD;
到-1和到4的距离之和;5;线段CD;
(6)表示![]() 点
点![]() 到1,2,3的距离之和
到1,2,3的距离之和
∴![]() 的最小值是2,此时
的最小值是2,此时![]() 2.
2.
故答案为:2;2.