题目内容
 已知如图:直角梯形ABCD中,AD∥BC,∠BAD=90°,BC=CD=26,sinC=
已知如图:直角梯形ABCD中,AD∥BC,∠BAD=90°,BC=CD=26,sinC=| 12 | 13 |
分析:作DE⊥BC,利用正弦函数和余弦函数的定义,求出CE和DE的值,再求出EB的值,根据梯形的面积公式计算即可.
解答: 解:作DE⊥BC,垂足为E.
解:作DE⊥BC,垂足为E.
∵CD=26,sinC=
,
∴
=
,
∴
=
,
∴DE=24.
根据勾股定理,CE=
=10.
BE=26-10=16.
即AD=16,
在梯形ABCD中,
S梯形ABCD=
(AD+BC)•24=
×(16+26)×24=42×12=504.
 解:作DE⊥BC,垂足为E.
解:作DE⊥BC,垂足为E.∵CD=26,sinC=
| 12 |
| 13 |
∴
| DE |
| CD |
| 12 |
| 13 |
∴
| DE |
| 26 |
| 12 |
| 13 |
∴DE=24.
根据勾股定理,CE=
| 262-242 |
BE=26-10=16.
即AD=16,
在梯形ABCD中,
S梯形ABCD=
| 1 |
| 2 |
| 1 |
| 2 |
点评:此题结合梯形的面积,考查了三角函数的定义,构造直角三角形,创设三角函数适用的条件是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
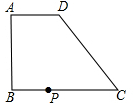 已知如图,直角梯形ABCD中,AD∥BC,AB⊥BC,AD=2,BC=DC=5,点P在BC上移动,则当PA+PD取最小值时,△APD中边AP上的高为
已知如图,直角梯形ABCD中,AD∥BC,AB⊥BC,AD=2,BC=DC=5,点P在BC上移动,则当PA+PD取最小值时,△APD中边AP上的高为 已知如图:直角梯形ABCD中,AD∥BC,∠BAD=90°,BC=CD=26,
已知如图:直角梯形ABCD中,AD∥BC,∠BAD=90°,BC=CD=26,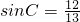 ,求:梯形ABCD的面积.
,求:梯形ABCD的面积.
 ,求:梯形ABCD的面积.
,求:梯形ABCD的面积.