题目内容
菱形的周长为24cm,且有一内角为120°,则这个菱形的面积为 cm2.
考点:菱形的性质
专题:
分析:作出图形,连接AC,根据菱形的对角线平分一组对角可得∠BAC=60°,判断出△ABC是等边三角形,再求出菱形的边长,根据等边三角形的性质求出BC边上的高,然后根据菱形的面积公式列式计算即可得解.
解答: 解:如图,连接AC,
解:如图,连接AC,
∵菱形的内角∠BAD为120°,
∴∠BAC=
×120°=60°,
∴△ABC是等边三角形,
∵菱形的周长为24cm,
∴菱形的边长为24÷4=6cm,
∴菱形ABCD的边BC上的高为6×
=3
cm,
菱形的面积=6×3
=18
cm2.
故答案为:18
.
 解:如图,连接AC,
解:如图,连接AC,∵菱形的内角∠BAD为120°,
∴∠BAC=
| 1 |
| 2 |
∴△ABC是等边三角形,
∵菱形的周长为24cm,
∴菱形的边长为24÷4=6cm,
∴菱形ABCD的边BC上的高为6×
| ||
| 2 |
| 3 |
菱形的面积=6×3
| 3 |
| 3 |
故答案为:18
| 3 |
点评:本题考查了菱形的性质,等边三角形的判定与性质,作辅助线构造出等边三角形是解题的关键,作出图形更形象直观.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目
已知方程x(x-1)=a的一个根是x=-1,则( )
| A、a=1 | B、a=±2 |
| C、a=2 | D、a=-2 |
在平面直角坐标系中,如果直线y=k1x与双曲线y=
有交点,那么k1和k2的关系是( )
| k2 |
| x |
| A、k1<0,k2>0 |
| B、k1>0,k2<0 |
| C、k1、k2同号 |
| D、k1、k2异号 |
| x-2 |
| A、x>2 | B、x≥2 |
| C、x≠2 | D、一切实数 |
 如图,等腰梯形ABCD中,AD=6,AB=CD=8,BC=15,且CD的中垂线l交BC于P点,连接PD.则四边形ABPD的周长为( )
如图,等腰梯形ABCD中,AD=6,AB=CD=8,BC=15,且CD的中垂线l交BC于P点,连接PD.则四边形ABPD的周长为( )| A、26 | B、27 | C、28 | D、29 |
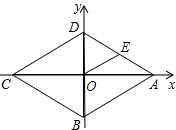 如图,菱形ABCD中,对角线AC、BD相关于点O,且AC=16,BD=12,E为AD的中点,点P在x轴正半轴上移动,若△POE为等腰三角形,则P的坐标是
如图,菱形ABCD中,对角线AC、BD相关于点O,且AC=16,BD=12,E为AD的中点,点P在x轴正半轴上移动,若△POE为等腰三角形,则P的坐标是