题目内容

①sin2A+cos2A=
 
，②tanA•cotA=
 
．
分析：画出直角三角形，根据定义即可证明．
解答：精英家教网解：如图：①∵sinA=
BC
AB
，cosA=
AC
AB
，
∴sin2A+cos2A=（
BC
AB
）2+（
AC
AB
）2=
BC2+AC2
AB2
=
AB2
AB2
=1；

②∵tanA=
BC
AC
，cotA=
AC
BC
，
∴tanA•cotA=
BC
AC
•
AC
BC
=1．
点评：此题考查了锐角三角函数的定义，只要画出图形即可列式计算．
练习册系列答案
相关题目
如图，已知在Rt△ABC中，∠C=90°，它的三边长分别为a，b，c，对于同一个锐精英家教网角A的正弦，余弦存在关系式sin2A+cos2A=1试说明．
解：∵sinA=
 
，cosA=
 
．
∴sin2A+cos2A=
 
，
∵a2+b2=c2，∴sin2A+cos2A=1．
（1）在横线上填上适当内容；
（2）若∠α为锐角，利用（1）的关系式解决下列问题．
①若sinα=
4
5
，求cosα的值；cosα=
3
5

②若sinα+cosα=1.1，求sinαcosα的值．sinαcosα=0.105．
下列说法中，正确的是（　　）
A、在Rt△ABC中，若tanA=
3
4
，则a=4，b=3
B、若三角形的三边之比为1：
3
：2，则三角形是直角三角形
C、对于锐角α，必有sinα＜cosα
D、在Rt△ABC中，∠C=90°，则sin2A+cos2B=1
（2012•衡阳）观察下列等式
①sin30°=
1
2
     cos60°=
1
2

②sin45°=
2
2
   cos=45°=
2
2

③sin60°=
3
2
    cos30°=
3
2

…
根据上述规律，计算sin2a+sin2（90°-a）=
1
1
．
在Rt△ABC中，∠C=90°，下列等式：（1）sin A=sin B；（2）a=c•sin B；（3）sin A=tan A•cos A；（4）sin2A+cos2A=1．其中一定能成立的有（　　）

观察下列等式

①sin30°=     cos60°=

②sin45°=   cos=45°=

③sin60°=    cos30°=

…

根据上述规律，计算sin2a+sin2（90°﹣a）=        ．

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

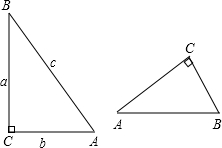精英家教网