题目内容
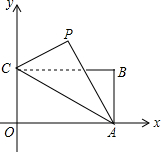 如图,在平面直角坐标系中,矩形OABC的长OA=
如图,在平面直角坐标系中,矩形OABC的长OA=| 3 |
(1)填空:A点坐标为
(2)若P,A两点在抛物线y=-
| 4 |
| 3 |
(3)设E(0,n)是y轴上的动点,过点E的直线y=
| 3 |
①当n<1,EM和EN的大小如何?为什么?
②当n为何值时,△MCN是以MN为斜边的直角三角形?
考点:二次函数综合题
专题:
分析:(1)利用翻折变换的性质以及锐角三角函数关系得出PD以及CE的长,进而得出答案;
(2)利用点P(
,
),A(
,0)在抛物线上,利用待定系数法求二次函数解析式进而得出C点是否在抛物线上;
(3)①首先得出MP′=NQ,进而得出△MEP′≌△NEQ,即可得出EM=EN;
②设y=
x+n与x轴交于点F,则∠OFE=60°,(即∠OEF=30°),若∠MCN=90°,则CE=EM=NE,进而得出答案.
(2)利用点P(
| ||
| 2 |
| 3 |
| 2 |
| 3 |
(3)①首先得出MP′=NQ,进而得出△MEP′≌△NEQ,即可得出EM=EN;
②设y=
| 3 |
解答: 解:(1)过点P作PD⊥AO于点D,交BC于点E,
解:(1)过点P作PD⊥AO于点D,交BC于点E,
∵矩形OABC的长OA=
,宽OC=1,将△AOC沿AC翻折得△APC,
∴A(
,0),tan∠CAO=
=
,PC=1,
∴∠CAO=30°,
∴∠OCA=60°,∠ACB=30°,
∴∠PCB=60°-30°=30°,
∴PE=
PC=
,EC=
=
,
∴PD=PE+ED=1+
=
,
∴P(
,
);
故答案为:(
,0),(
,
);
(2)∵点P(
,
),A(
,0)在抛物线上,
∴
,
解得:
,
∴抛物线解析式为:y=-
x2+
x+1,
已知C点坐标为;(0,1),
∵-
×02+
×0+1=1,
∴点C在此抛物线上;
(3)①EM=EN,
理由:作MP′⊥y轴,NQ⊥y轴,垂足分别为P′、Q,
由
,
解得:x=±
(n<1),
即|xM|=|xN|,
∴MP′=NQ,
∴在△MEP′和△NEQ中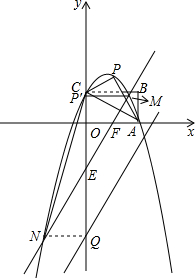
,
∴△MEP′≌△NEQ(AAS),
∴EM=EN;
②设y=
x+n与x轴交于点F,
则∠OFE=60°,(即∠OEF=30°),
∴ME的长是MP′的2倍,
即ME=
×2,
若∠MCN=90°,
则CE=EM=NE,
∴1-n=
×2,
解得;n1=1,n2=-2,
∵n<1,∴n=-2,
∴当n=-2时,△MCN是以MN为斜边的直角三角形.
 解:(1)过点P作PD⊥AO于点D,交BC于点E,
解:(1)过点P作PD⊥AO于点D,交BC于点E,∵矩形OABC的长OA=
| 3 |
∴A(
| 3 |
| 1 | ||
|
| ||
| 3 |
∴∠CAO=30°,
∴∠OCA=60°,∠ACB=30°,
∴∠PCB=60°-30°=30°,
∴PE=
| 1 |
| 2 |
| 1 |
| 2 |
1-(
|
| ||
| 2 |
∴PD=PE+ED=1+
| 1 |
| 2 |
| 3 |
| 2 |
∴P(
| ||
| 2 |
| 3 |
| 2 |
故答案为:(
| 3 |
| ||
| 2 |
| 3 |
| 2 |
(2)∵点P(
| ||
| 2 |
| 3 |
| 2 |
| 3 |
∴
|
解得:
|
∴抛物线解析式为:y=-
| 4 |
| 3 |
| 3 |
已知C点坐标为;(0,1),
∵-
| 4 |
| 3 |
| 3 |
∴点C在此抛物线上;
(3)①EM=EN,
理由:作MP′⊥y轴,NQ⊥y轴,垂足分别为P′、Q,
由
|
解得:x=±
| ||
| 2 |
即|xM|=|xN|,
∴MP′=NQ,
∴在△MEP′和△NEQ中

|
∴△MEP′≌△NEQ(AAS),
∴EM=EN;
②设y=
| 3 |
则∠OFE=60°,(即∠OEF=30°),
∴ME的长是MP′的2倍,
即ME=
| ||
| 2 |
若∠MCN=90°,
则CE=EM=NE,
∴1-n=
| ||
| 2 |
解得;n1=1,n2=-2,
∵n<1,∴n=-2,
∴当n=-2时,△MCN是以MN为斜边的直角三角形.
点评:此题主要考查了锐角三角函数关系以及全等三角形的判定与性质以及待定系数法求二次函数解析式等知识,利用数形结合以及直角三角形的性质得出EC=ME是解题关键.

练习册系列答案
相关题目
下列事件中是必然事件的为( )
| A、方程x2-x+1=0有两个不等实根 | ||
B、
| ||
| C、圆的切线垂直于圆的半径 | ||
| D、旋转后的图形与原来图形对应线段平行且相等 |
已知?ABCD中,∠A=40°,则下列判断正确的是( )
| A、∠B=140°,∠C=140° |
| B、∠C=140°,∠D=140° |
| C、∠B=140°,∠D=140° |
| D、∠B=40°,∠D=140° |
 如图,⊙O直径AB和弦CD相交于点E,AE=2,EB=6,∠DEB=30°,求弦CD长为
如图,⊙O直径AB和弦CD相交于点E,AE=2,EB=6,∠DEB=30°,求弦CD长为 如图,△A1A2B是直角三角形,∠A1A2B=90°,且A1A2=A2B=4,A2A3⊥A1B,垂足为A3,A3A4⊥A2B,垂足为A4,A4A5⊥A3B,垂足为A5,A5A6⊥A4B,垂足为A6,一直按此做去,…则△AnAn+1B的面积为
如图,△A1A2B是直角三角形,∠A1A2B=90°,且A1A2=A2B=4,A2A3⊥A1B,垂足为A3,A3A4⊥A2B,垂足为A4,A4A5⊥A3B,垂足为A5,A5A6⊥A4B,垂足为A6,一直按此做去,…则△AnAn+1B的面积为