题目内容
⊙O1与⊙O2的半径分别为2和3,若两圆外离,则圆心距d的取值范围是 .
考点:圆与圆的位置关系
专题:
分析:本题直接告诉了两圆的半径及两圆位置关系,根据数量关系与两圆位置关系的对应情况便可直接得出答案.外离,则P>R+r;外切,则P=R+r;相交,则R-r<P<R+r;内切,则P=R-r;内含,则P<R-r.(P表示圆心距,R,r分别表示两圆的半径).
解答:解:根据题意,得
R+r=2+3=5,
∵两圆外离,
∴圆心距d>5,
故答案为:d>5.
R+r=2+3=5,
∵两圆外离,
∴圆心距d>5,
故答案为:d>5.
点评:本题考查了圆与圆的位置关系,由数量关系及两圆位置关系求圆心距的取值范围是常见的题型之一,难度不大.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
 如图,从正面看由相同的小正方体搭成的几何体,所得到的平面图形是( )
如图,从正面看由相同的小正方体搭成的几何体,所得到的平面图形是( )A、 |
B、 |
C、 |
D、 |
在平面直角坐标系中,对于平面内一点(m,n)规定以下两种变换,
①f(m,n)=(m,-n),如f(2,1)=(2,-1);
②g(m,n)=(-m,-n),如g(2,1)=(-2,-1).
按照以上变换,则经过点f[g(3,4)],点g[f(-3,2)]的直线方程为( )
①f(m,n)=(m,-n),如f(2,1)=(2,-1);
②g(m,n)=(-m,-n),如g(2,1)=(-2,-1).
按照以上变换,则经过点f[g(3,4)],点g[f(-3,2)]的直线方程为( )
A、y=-
| ||
B、y=
| ||
C、y=-
| ||
D、y=
|
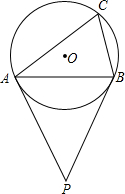 如图,已知PA、PB分别切⊙O于A、B,点C在⊙O上,∠BCA=75°,则∠P=
如图,已知PA、PB分别切⊙O于A、B,点C在⊙O上,∠BCA=75°,则∠P= 如图△ABC中,∠A=36°,AB=AC,且BD平分∠ABC交AC于点D,若AB=2,则AD=
如图△ABC中,∠A=36°,AB=AC,且BD平分∠ABC交AC于点D,若AB=2,则AD=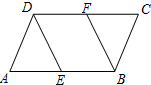 如图,在平行四边形ABCD中,AE=CF.求证:
如图,在平行四边形ABCD中,AE=CF.求证: