题目内容
5. 如图,△ABC的中线BD、CE交于点O,F、G分别是BO、CO的中点,试说明EF${\;}_{=}^{∥}$DG.
如图,△ABC的中线BD、CE交于点O,F、G分别是BO、CO的中点,试说明EF${\;}_{=}^{∥}$DG.
分析 连接OA,由已知条件得出EF是△ABO的中位线,DG是△ACO的中位线,由三角形中位线定理得出EF∥OA,EF=$\frac{1}{2}$OA,DG∥OA,DG=$\frac{1}{2}$OA,即可得出结论.
解答 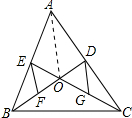 证明:连接OA,如图所示:
证明:连接OA,如图所示:
∵△ABC的中线BD、CE交于点O,F、G分别是BO、CO的中点,
∴EF是△ABO的中位线,DG是△ACO的中位线,
∴EF∥OA,EF=$\frac{1}{2}$OA,DG∥OA,DG=$\frac{1}{2}$OA,
∴EF${\;}_{=}^{∥}$DG.
点评 本题考查了三角形中位线定理;熟练掌握三角形中位线定理,通过作辅助线证出三角形中位线是解决问题的关键.

练习册系列答案
相关题目
20.已知x=-2015,计算|x2+2014x+1|+|x2+2016x-1|的值为( )
| A. | 4030 | B. | 4031 | C. | 4032 | D. | 4033 |
10.下列运用等式性质进行的变形,其中不正确的是( )
| A. | 如果a=b,那么a+3=b+3 | B. | 如果a=b,那么a-$\frac{1}{2}$=b-$\frac{1}{2}$ | ||
| C. | 如果a=b,那么ac=bc | D. | 如果a=b,那么$\frac{a}{c}=\frac{b}{c}$ |



