题目内容
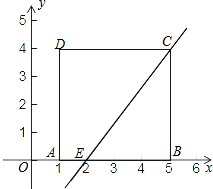 正方形ABCD的边长为4,将此正方形置于平面直角坐标系中,使AB边落在X轴的正半轴上,且A点的坐标是(1,0).
正方形ABCD的边长为4,将此正方形置于平面直角坐标系中,使AB边落在X轴的正半轴上,且A点的坐标是(1,0).(1)直线y=
| 4 |
| 3 |
| 8 |
| 3 |
(2)若直线l经过点E,且将正方形ABCD分成面积相等的两部分,求直线l的解析式;
(3)若直线l1经过点F(-
| 3 |
| 2 |
| 2 |
| 3 |
考点:一次函数综合题
专题:
分析:(1)求得C的坐标,以及E的坐标,则求得AE的长,根据直角梯形的面积公式即可求得四边形的面积;
(2)经过点E且将正方形ABCD分成面积相等的两部分的直线与CD的交点F到C的距离一定等于AE,则F的坐标可以求得,利用待定系数法即可求得直线EF的解析式;
(3)根据直线l1经过点F(-
,0)且与直线y=3x平行,知k=3,把F的坐标代入即可求出b的值即可得出直线11,同理求出解析式y=2x-3
,进一步求出M、N的坐标,利用三角形的面积公式即可求出△MNF的面积..
(2)经过点E且将正方形ABCD分成面积相等的两部分的直线与CD的交点F到C的距离一定等于AE,则F的坐标可以求得,利用待定系数法即可求得直线EF的解析式;
(3)根据直线l1经过点F(-
| 3 |
| 2 |
| 1 |
| 3 |
解答:解:(1)在y=
x-
中,
令y=4,即
x-
x=4,
解得:x=5,则B的坐标是(5,0);
令y=0,即
x-
=0,
解得:x=2,则E的坐标是(2,0).
则OB=5,OE=2,BE=OB-OA=5-2=3,
∴AE=AB-BE=4-3=1,
边形AECD=
(AE+CD)•AD=
(4+1)×4=10;
(2)经过点E且将正方形ABCD分成面积相等的两部分,则直线与CD的交点F,必有CF=AE=1,则F的坐标是(4,4).
设直线的解析式是y=kx+b,则
,
解得:
.
则直线l的解析式是:y=2x-4;
(3)∵直线l1经过点F(-
,0)且与直线y=3x平行,
设直线11的解析式是y1=kx+b,
则:k=3,
代入得:0=3×(-
)+b,
解得:b=
,
∴y1=3x+
,
已知将(2)中直线l沿着y轴向上平移
个单位,则所得的直线的解析式是y=2x-4+
,
即:y=2x-3
,
当y=0时,x=
,
∴M(
,0),
解方程组
得:
,
即:N(-7
,-19),
S△NMF=
×[
-(-
)]×|-19|=
.
答:△NMF的面积是
.
| 4 |
| 3 |
| 8 |
| 3 |
令y=4,即
| 4 |
| 3 |
| 8 |
| 3 |
解得:x=5,则B的坐标是(5,0);
令y=0,即
| 4 |
| 3 |
| 8 |
| 3 |
解得:x=2,则E的坐标是(2,0).
则OB=5,OE=2,BE=OB-OA=5-2=3,
∴AE=AB-BE=4-3=1,
边形AECD=
| 1 |
| 2 |
| 1 |
| 2 |
(2)经过点E且将正方形ABCD分成面积相等的两部分,则直线与CD的交点F,必有CF=AE=1,则F的坐标是(4,4).
设直线的解析式是y=kx+b,则
|
解得:
|
则直线l的解析式是:y=2x-4;
(3)∵直线l1经过点F(-
| 3 |
| 2 |
设直线11的解析式是y1=kx+b,
则:k=3,
代入得:0=3×(-
| 3 |
| 2 |
解得:b=
| 9 |
| 2 |
∴y1=3x+
| 9 |
| 2 |
已知将(2)中直线l沿着y轴向上平移
| 2 |
| 3 |
| 2 |
| 3 |
即:y=2x-3
| 1 |
| 3 |
当y=0时,x=
| 5 |
| 3 |
∴M(
| 5 |
| 3 |
解方程组
|
|
即:N(-7
| 5 |
| 6 |
S△NMF=
| 1 |
| 2 |
| 5 |
| 3 |
| 3 |
| 2 |
| 361 |
| 12 |
答:△NMF的面积是
| 361 |
| 12 |
点评:本题主要考查了一次函数的特点,待定系数法求一次函数的解析式,一次函数图象上点的特征,平移的性质等知识点,解此题的关键是能综合运用上面的知识求一次函数的解析式.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
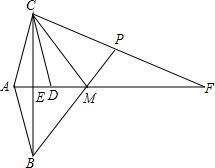 已知:如图,三角形ABM与三角形ACM关于直线AF成轴对称,三角形ABE与三角形DCE关于点E成中心对称,点E、D、M都在线段AF上,BM的延长线交CF于点P.
已知:如图,三角形ABM与三角形ACM关于直线AF成轴对称,三角形ABE与三角形DCE关于点E成中心对称,点E、D、M都在线段AF上,BM的延长线交CF于点P.