题目内容
对于任意实数a、b,定义一种运算“★”:a★b=a2-3a+b.若m★2=6,则实数m的值是 .
考点:解一元二次方程-因式分解法
专题:新定义
分析:根据已知得出m★2=6即为m2-3m+2=6,进而利用十字相乘法分解因式得出即可.
解答:解:∵a★b=a2-3a+b.若m★2=6,
∴m2-3m+2=6,
∴m2-3m-4=0,
∴(m-4)(m+1)=0,
解得:m1=4,m2=-1.
故答案为:-1,4.
∴m2-3m+2=6,
∴m2-3m-4=0,
∴(m-4)(m+1)=0,
解得:m1=4,m2=-1.
故答案为:-1,4.
点评:此题主要考查了因式分解法解一元二次方程,正确将方程分解因式是解题关键.

练习册系列答案
相关题目
下列化简正确的是( )
A、
| ||||||
B、
| ||||||
C、3
| ||||||
D、
|
甲数的2倍比乙数大3,甲数的3倍比乙数的2倍小1,若设甲数为x,乙数为y,则根据题意可列出的方程组为( )
A、
| |||||
B、
| |||||
C、
| |||||
D、
|

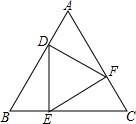 如图,△ABC是边长为6的等边三角形,DE⊥BC于E,EF⊥AC于F,FD⊥AB于D,则AD=
如图,△ABC是边长为6的等边三角形,DE⊥BC于E,EF⊥AC于F,FD⊥AB于D,则AD=